In: D. S. Levine and M. Aparicio (Eds.), Neural Networks for Knowledge Representation and Inference. Lawrence Erlbaum Associates, Hillsdale, New Jersey, 1994.

Chapter 13

Toward a Theory of Learning and Representing Causal Inferences in Neural Networks

George E. Mobus

University of North Texas

Current Affiliation: University of Washington, Tacoma, WA, USA

1. INTRODUCTION

We perceive the world to operate according to a fundamental principle of causality in spite of the seeming chaotic behavior of nature. The Universe seems to be orderly and we are able to comprehend this order at some very deep level. Some events (states of processes) cause other events, which, in turn, cause still other events. And we find, generally, that certain events tend to be associated with certain other events, which is to say, there is regularity to the Universe. This principle lies at the root of cognition and is the basis for scientific investigation. It can be viewed as the language of nature.

It is useful to view languages as having a syntactic as well as a semantic level of organization. The syntax of causality is a set of rules, the grammar if you will, that describes the temporal and spatial relationships that must exist between two events, say A and B, in order to instantiate an inference of the form A ==> B (A causes B). At the semantic level, we are provided with the means to reason about the world knowing that A ==> B. At the very base of this ability is the capacity to predict the future. That is, if A is observed we can infer that B will occur. Furthermore, we infer that B will occur within some specific temporal window. This capacity is fundamental to survival in the natural world. The realization of such a capacity involves several key issues. How is the syntax to be represented? How are these representations to be acquired from experience? And how may they be used semantically to reason from the state of the environment to some future state - how are they accessed and how are they processed?

During the past decade some real progress has been made in understanding how neural systems function (Alkon, 1987, 1989; Getting, 1980; Jaffe and Johnston, 1990; Kandel and Schwartz, 1982; Small, Kandel, and Hawkins, 1989; Starmer, 1987). Additional insights into the details of neural representation, learning and processing have been gained by building formal models of neural networks (Alkon, Blackwell, Barbour, Rigler, and Vogl, 1990; Buonomano, Baxter, and Byrne, 1990; Byrne and Gingrich, 1989; Byrne, Gingrich, and Baxter, 1990; Gelperin, Hopfield, and Tank, 1985; Klopf, 1988; Klopf and Morgan, 1990; Koch and Segev, 1989; Morgan, Patterson, and Klopf, 1990; Rumelhart and McClelland, 1986; Sejnowski, Chattarji, and Stanton, 1989). Here I want to explore an approach to representing and learning causal relations in a formal neural network in which the syntax of causality is the language of neural organization.

1.1. BACKGROUND

To begin understanding how the human mind perceives and reasons about the world, how it captures and uses the regularity of nature, we might ask how it is that causality, or more precisely, causal relations, are encoded in the brain. How does the brain represent causal relations and how are these representations learned? To make the task approachable we note first that all animal life is faced with the same problem of discovering and using regularity in the quest for survival and propagation. Thus by studying primitive (that is phylogenetically simpler) brains we may discern some mechanisms for such encoding which will be found to be invariant across the phylogenetic spectrum.

Specifically, the learning model of conditioning, demonstrable in some very primitive animals, is an operational version of learning and representing a causal relation. The outline of neural and even molecular substrates of conditioned learning has begun to emerge from the laboratories of neuroscience (Alkon, 1987; Kandel and Schwartz, 1982; Small et al., 1989). Connectionist views of classical and operant conditioning, likewise, have provided computational models which may aid in the discovery of these invariants (Carpenter and Grossberg, 1987a, 1987b; Grossberg, 1987; Sutton, 1988; Sutton and Barto, 1987, 1991). Such models, constrained by the wealth of neurophysiological and psychophysical data regarding conditioning, provide valuable insights into the principles of learning and may produce further hypothesis for investigation (Getting, 1980). Additionally, one hopes to find clues that will aid in the construction of machine-based mechanisms with animal-like learning competence (Anderson, Merrill, and Port, 1989; Elman and Zipser, 1988; Morgan et al., 1990; Rumelhart and McClelland, 1986).

In this chapter I introduce a learning mechanism called an Adaptrode (Mobus, 1990; Mobus and Fisher, 1990; Mobus, Cherri, and Fisher, 1993) which solves an important problem in representing temporal information in neurons. A neural network in which Adaptrodes are used to process synaptic efficacy and adaptive thresholds is shown to be competent at the conditioned learning task. The thrust of this chapter, however, is to show how this approach satisfies the temporal constraints of causality, suggesting that conditioned learning should be considered a basic form of causal relation learning. A number of workers hold that conditioning represents a basic mechanism for more complex learning task (Mackintosh, 1983; Staddon and Zhang, 1991). If this is so, then it constitutes a basis for understanding the more advanced, that is, cognitive, forms of perceiving causal relations that allow us to reason about the world.

1.2. TEMPORAL CONSTRAINTS OF CAUSALITY

Causality imposes several important temporal constraints on the form of any derived inference (Dretske, 1988; Mackintosh, 1983). First, of course, the fact that the event A must precede the event B in order for us to say that A is a cause of B. We rarely say that the breaking window caused the ball to be thrown. More precisely we require that the onset of A precede the onset of B by some Delta-t > 0. We can relax this constraint somewhat by requiring (or allowing) that A almost always precedes B, where "almost always" refers to some statistically defined frequency. There may be other causes of B and the occurrence of A may not always result in B. The constraint, however, strongly requires that B never precedes A, at least within some defined latency period, which is to say the temporal relation is one-way.

Another, related but technically different, constraint is that of temporal contiguity. The events must occur within a temporal window of opportunity. This window is defined by the context of events and the memory retention of event A. Thus it is not that B must occur shortly after A, but rather, B must occur after A but before the memory of A fades and no intervening event changes the context established by A. This is a subtle aspect of contiguity not often fully appreciated. Memory plays an important role in inference of causality. If B occurs too long after A has occurred, then the linkage between them is weakened.

A third constraint has to do with computing the correlation of A and B over time (contingency). In probabilistic causality we allow that the occurrence of A may increase the probability of the occurrence of B. The event B can have other, unobserved causes. Thus we infer a causal relation between A and B only if the frequency of co-occurrence is sufficient to the purpose (note this need not be a majority of the times). The temporal constraint, thus imposed, is that a sufficient period has to pass in which multiple occurrences of A and B can be experienced. We note again that memory is involved in keeping a count of the co-occurrences and that memory must persist over the time scale of the "sufficient" observation period.

These constraints, implicit in the prototypical causality rules, underscore the importance of the role of time in learning, representing and processing (reasoning) derived causality rules. Furthermore, we can see from the above discussion that temporal information extends across many time scales. It is not sufficient to deal with just the time scale of the real-time events (A and B). Therefore the nervous system must employ mechanisms which encode temporal information in multiple time domains.

1.3. CONDITIONED LEARNING AS A "SIMPLE" FORM OF CAUSAL REPRESENTATION

One form of learning task that is well documented and embodies causality rules is conditioned learning (Alkon, 1987; Alkon, Vogl, Blackwell, and Tam, 1991; Aparicio, 1988; Dretske, 1988; Gelperin et al., 1985; Grossberg, 1991; Klopf, 1988; Mackintosh, 1983; Pavlov, 1927; Sutton and Barto, 1987, 1991; Tesauro, 1986). In this paradigm (of which there are two flavors) the animal learns to associate an event such as an environmental cue with a behavior (or with a consequence). Though the notion behind conditioning has its origin in laboratory experiments, the general idea of conditioned learning and how it benefits the animal in its natural environment is fairly straightforward. If an environmental event (cue) which is neutral with respect to the animal's survival, is found by experience to precede another event which has direct survival impact, such as the availability of food or pain caused by a wound, then the animal forms a lasting association between those events and can use the prior event to predict the occurrence of the second event. Such predictive ability allows the animal to respond more quickly to the impending meaningful event. This can be seen in the experimental paradigm called classical or Pavlovian conditioning (Pavlov, 1927). The animal learns to associate a conditionable stimulus (CS) with an unconditionable (hard wired) stimulus-response (UCS/UCR). The association results in the UCR being elicited upon presentation of the CS alone. The animal has learned to respond to the CS as if it were the UCS.

The second form of this type of learning involves the stochastic emission of a behavior which reliably produces some beneficial result (for the animal) in the environment. The animal learns to associate the behavior with the beneficial result and can, in principle, emit the behavior by choice in order to elicit the result. This latter form of learning, termed operant (or instrumental) conditioning, depends on a contextual situation, for example a physiological drive, which creates the condition in which the result will be beneficial. In the laboratory setting, animals are kept hungry so that they are "motivated" to press levers or buttons so as to receive a food pellet.

How are these conditioned learning tasks to be viewed as simple causal representations? There is the philosophical side to this question wherein we can speculate over the animal's perceptions and beliefs about cause and effects (Dretske, 1988). However, I am more interested in an operational view in which the animal behaves as if a cause and effect relation has been learned. Whether A (the CS) actually causes B (the UCS) which in turn causes C (the UCR) in an objective sense, or is the perception of the animal is of little concern just now. The point is that the animal responds to A (with C) as if a causal chain had been established. >From the standpoint of behavior, there exists the inference of a causal chain.

The balance of this chapter focuses on the way in which neural networks can encode the temporal and associative rules of causality. This is examined at the level of conditioned response learning where it will be shown that a neural architecture can be built in which the prototypical rules, in particular the temporal constraints, of causality can be instantiated in representations of events which are causes (predictors) and events which are effects (consequences or reinforcers). If it is true that conditioned learning is a fundamental basis for higher forms of learning as has been suggested, then this approach may fulfill the promise of directing us toward a theory of causal inference learning and reasoning in higher cognitive processes.

2. REPRESENTING TIME IN NEURAL NETWORKS

As I hope has been established, the role of time in causal inference is central and crucial. In order to meet the temporal constraints of causality we must show how a neural network can encode temporal knowledge, integrated with spatial associative knowledge, such that information processing produces the correct inferential result. In this section I briefly review some methods which have been employed to incorporate temporal representation in neural networks. I then introduce in the next section a novel algorithm for producing adaptive response as the basis for learning in networks. In section 4 I show the results of simulated neural networks based on this algorithm in which conditioned learning is demonstrated.

2.1. PRIMACY OF ASSOCIATIVITY

The vast majority of learning rules that are used in neural network architectures have at their base the assumption of associativity as the driving influence in changing the edge weights associated with processing element inputs. What this means, simply, is that in order for a weight to be modified, there must be some kind of correlation between two or more independent signals in the processing element. These can be, for example, an input correlated with the output of the element such as the Hebb rule (Hebb, 1949; Hertz, Krogh, and Palmer, 1991), input correlated with an error (difference between the output and a desired output or delta rule, Widrow and Hoff, 1960), or two inputs (local interaction rule, Alkon et al., 1990). Such rules can be further modified to take into account the time derivative of the signals (Klopf, 1988; Kosko, 1986) or the error derivative in the case of the generalized delta rule (Rumelhart, Hinton, and Williams, 1985). However, the change in a weight is still dependent on the activity of two or more signals.

This form of associativity is a spatial encoding mechanism. A large number of neural network applications have addressed the issues of pattern learning, classification, and recognition. Their successes have led to what seems to be a general consensus that learning rules must, at their base, be associative. As a result this has led to an interesting problem: How to represent temporal knowledge when the basic rule is associative (Elman, 1990).

2.2. ADDING TEMPORAL REPRESENTATION TO ASSOCIATIVE-BASED NETWORKS

A typical solution to this problem has been an attempt to add temporal representation to an otherwise associative learning scheme. The earliest efforts attempted to construct architectures in which time could be represented by a spatial analogue. For example an avalanche circuit could be used to represent time steps in a sequence (Grossberg, 1982).

Another method for representing temporal information at the level of the network is through recurrent loops and/or time delay units (see Hertz et al., 1991, esp. Section 7.3). In the simplest version a neuron excites itself through a loop with inherent decay. Grossberg (1991 for an excellent review) and others have used this method to instantiate a short-term memory (STM) function at the level of individual neurons. An associative rule is still used to update the weights (called long-term memory - LTM) on the other inputs to the neuron.

Recurrency can be used on a network-wide basis as well. One neuron can excite (through a non-learning connection) another neuron which can, in turn, excite the former directly or through a chain of neurons. This method has been used by a number of workers using the backpropagation learning method. Context units which feed back historical states to earlier layers in the network act as a memory of prior input and processing, thus having an impact on the current processing (Elman, 1990). Systems of this kind have been shown to be able to learn and recognize and/or generate sequences of spatially extended patterns.

2.3. ADDING ASSOCIATIVITY TO TEMPORAL REPRESENTATION - AN ALTERNATIVE

In these systems some form of temporal representation is added to a network architecture based on an associative learning rule. An alternative approach would be to add associative encoding to a temporally based learning rule. I had been interested in the biological phenomenon of adaptive response in which an animal modifies its response to a stimulus based on the time course behavior of that stimulus. This is a fundamentally nonassociative phenomena which can become associative through modulation processes. From this work the outlines of the Adaptrode model emerged and were more recently refined in Paul Fisher's lab at the University of North Texas.

The problem of temporal representation is more complex than simply representing sequences. Perhaps the most important aspect of temporally extended phenomena is that modulation occurs over multiple time scales. The meaning or impact of real-time events can be modified by a longer time course activity of those events. A simple example of adaptive response lets us see this. People who decide to go into athletic training experience adaptive response of their muscles. The real time response of the body to athletic demand (performance) changes with time and training. If a rigorous training schedule is maintained the athlete's muscles strengthen and increase in bulk as new tissue is created. This occurs only if the demand schedule is maintained over an extended time period. The muscles come to expect an increase in work load as a result of past experience. They adapt to the expected level of demand. This is a form of learning which is based primarily on activity and time. There are short-term effects, intermediate-term effects and long-term effects that come into play.

Muscle growth however will be constrained, or modulated, by associative factors such as nutrition. Learning takes place if these factors are satisfied. Thus adaptive response is a model of learning in which associative factors act as modulators to an otherwise temporal encoding process.

Could adaptive response be a biologically plausible basis for learning in neural networks? More to the point, could this phenomenon be the basis for efficacy weight updating of synapses, thus bringing temporal representation from the level of a neuron (self-excitation) to the level of the synapse? If so, could the temporal representation meet the criteria of causal inference, which from my prior arguments means conditioned learning?

3. THE ADAPTRODE MODEL

3.1. SIGNALS

The ultimate source of activating signals in a neural network is the real world. The events that trigger these signals are stochastic, episodic and sporadic. It should be noted that the real world also includes the body of an animal (with respect to its brain - the neural network). Signals originating from internal body sources may have similar episodic characteristics, though the episodes may be superposed on periodic carriers.

We represent signals in this model by a train of spikes of constant pulse width and amplitude. A maximum frequency bounds the upper limit of signal strength and information is encoded by frequency modulation within this dynamic range. In reality information can be encoded in multiple temporal domains. The presence or absence of a pulse in a sample window (1 or 0) communicates information in one time domain. But pulses can be grouped in burst patterns with characteristic durations and inter-burst periods. This gives rise to a wide variety of encoding possibilities. For example, within a burst the frequency can be modulated giving rise to a unique integrated burst envelope. Burst lengths may change over a long time scale. The frequency of bursts may change over a long time scale.

What is common to all of these possibilities is the temporal properties of the signal. The Adaptrode is a mechanism for recording the time averaged activity of the signal in multiple time domains with the assumption that these domains are coupled. In this model we attempt to capture the time course behavior of a signal as a prerequisite to associative modulation.

3.2. RESPONSE UNIT

An Adaptrode is comprised of two basic module types. One of these, the weight vector unit, may be present in multiple versions. The other type, the response unit occurs only once per Adaptrode.

The response unit provides the "read-out" of memory in the Adaptrode. The current value of memory is made available on the response line by virtue of current or recent input to the Adaptrode. That is, the response output is a function of input and the memory of the system. Fig. 13.1(a) shows a diagrammatic representation of the response unit. An input signal at x⁰ = 1, at time step t, regenerates an active memory trace on the response line, r, given by

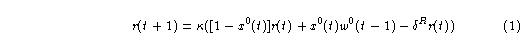
where

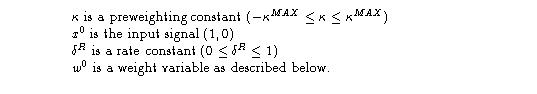
Fig. 13.1. (a) The response unit. From input signals x⁰ and w⁰ the unit computes a graded response output r. (b) A typical weight unit. An Adaptrode contains 1 to L+1 such units. Weight signals constitute the time domain memory of the system.

Each time the input goes to 1, the response signal is set to the current value of w⁰ multiplied by the constant κ. If the latter is negative then the response is negative. In the context of a synapse, this amounts to an inhibitory signal. At all other times (when x⁰ is approximately 1) the response will decay exponentially fast by the rate constant δ^R.

The response unit gives a memory read-out in response to input. The response may last for some period after a transient input goes to zero depending on the rate of decay.

3.3. REPRESENTATION - ENCODING SIGNALS AS TIME AVERAGES IN MULTIPLE TIME DOMAINS

We are interested in the way in which the input signal has varied over multiple time scales. Each of these scales is called a domain and is characterized by a set of rate constants which govern the learning and forgetting. Memory will be stored as a form of time average of the signal history from the prior domain. That is, one storage term holds a time average of the real-time signal, the next will hold the time average of the first, another holds the average of the second and so on over increasing time domains. Mostly for historical reasons this storage mechanism is called the weight vector (not to be confused with a weight vector of a single neuron) of the Adaptrode.

3.4. THE WEIGHT VECTOR UNIT: POTENTIATION

Each weight in the weight vector should more properly be thought of as a signal that varies over an increasing time scale. The time domains are indexed by k = {0, 1, ..., L}, where L is the longest time domain. A superscript is used to index weight signals, that is, w⁰, w¹,..., w^k, ..., w^L. Each component of the vector is said to occupy a level in the Adaptrode. Higher levels mean longer time domains. The zeroth weight signal is what was used above to compute the response signal. Fig. 13.1(b) shows a typical weight module in which the weight signal, w^k, is computed. The change in any w^k value over time is given by

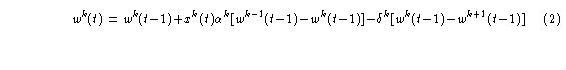
where

    α^k, δ^k are rate constants;
    x^k is an input signal at level k;

and

    w^k-1 = w^max, if k = 0,    w^k-1, otherwise        (3);
    w^k+1 = w^equil, if k = L, w^k+1, if k < L.        (4).

In the case where k = 0, the input signal, x⁰, is that which I described above, a pulse coded signal corresponding to neural action potential spike trains. Other input signals, x^k, are described below. The value of w^k-1 at level 0 is a special case, the constant w^max. This constant is generally set to one (1), representing the maximum of some arbitrary scale. It can be shown that for appropriate values of α⁰ and δ⁰, w⁰ encodes a lingering memory trace of the input signal which decays exponentially over time if the signal goes to zero.

A single level Adaptrode does not seem very interesting from the standpoint of memory. The slight lingering trace would soon decay leaving a weight value asymptotically close to zero. However, a multilevel Adaptrode has interesting properties. Each subsequent (higher) level records the time average of the prior level. This in turn decays at a much slower rate. The method by which this takes place is computationally inexpensive but quite effective. It can be seen by Equation (2) that the k^th weight is pulled up by the (k-1)^th weight by an amount proportional to the distance these two are apart and by the rate constant α^k. Thus, as long as the (k-1)^th level is excited (raised above the k^th level) there will be a pulling force exerted on w^k to raise it. Conversely, the k^th weight will be pulled downward by the (k+1)^th weight by an amount proportional to their distance apart and the decay constant δ^k.

At any moment then, the k^th weight signal is pulled between two opposing forces, which themselves vary over time. The net effect of this process is that the k^th level weight is buoyed from below by the (k+1)^th weight and bounded from above by the (k-1)^th weight. The buoying effect provided by the (k+1)^th level weight is the operant condition for multi-term memory. By raising the floor of the k^thlevel weight, likewise the floor of the (k-1)^th weight is raised as well. This proceeds all the way back to w⁰. And this is, so to speak, the payoff. It is w⁰ which is used to compute the read-out or response, r. Thus, if w⁰ is maintained for longer periods at a higher value, it means that the response will start from a higher value. In a competitive situation the Adaptrode with the higher starting value is more likely to win. Additionally, in the dynamics of w⁰, a higher starting value means that w⁰ will respond (grow) a little more quickly on new input. This is because the floor toward which it tends to decay by being raised, exerts a weaker force on the decay side. It thus rises to new heights and does so more rapidly. Fig. 13.2 shows a graph of the behavior of w⁰, w¹ and w² of a three level Adaptrode with two spaced short bursts of signal at x⁰ (all x^k = 1) Note how the peak of w⁰ on the second burst is higher then on the first.

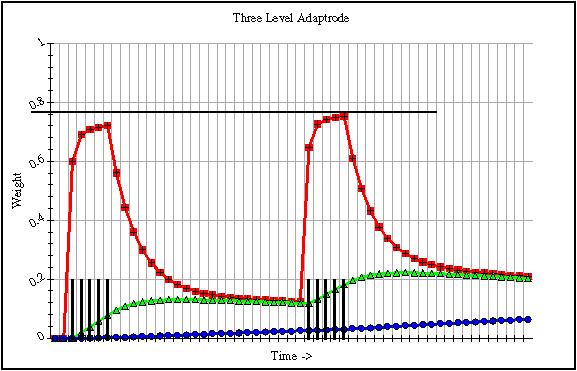
Fig. 13.2. A graph of weight signals for a three-level Adaptrode. α andδ values were chosen to accentuate the behavior for purposes of showing in a graph.

3.5. ASSOCIATIVITY: POTENTIATION GATING AND HURDLING THE GATE

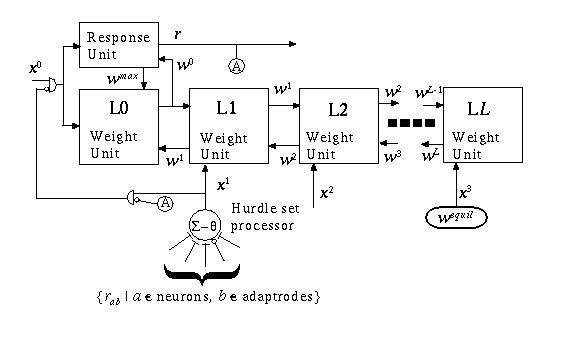
Fig. 13.3. Schematic layout of an Adaptrode. Weight units are labeled L0 through LL. There is only one Response unit per Adaptrode as presently discussed. A hurdle set processor takes as its input, the output from response units of any Adaptrode, including its own. If the sum of these inputs exceeds a set gate threshold, the unit outputs a one (1). A special logic circuit (AND gates) is shown that enforces the priority in time of the x⁰ signal over any x^k.

Hurdling the gate permits potentiation of the k^thlevel in an Adaptrode. The hurdle is determined by response signals from one or more Adaptrodes. No learning can occur in the first Adaptrode unless the hurdle set Adaptrode(s) is sufficiently active. This establishes a correlation requirement which allows temporal encoding if met. By selecting the appropriate level in the learning Adaptrode and appropriate source Adaptrodes whose input signals vary over the time scale of interest, one can create short-term to long-term correlation criteria which must be met to obtain learning in the appropriate temporal domain.

One last consideration which establishes the one-way temporal constraint required by causality should be noted. In Fig. 13.3 a logic circuit (and an equivalent processing element circuit) is shown which prevents the x⁰ signal from reaching the Adaptrode if a hurdle signal (x¹ in the figure) is already active when r is not active. The purpose of this circuit is to ensure that the Adaptrode has already been stimulated by the x⁰ signal prior to the arrival of signals which give rise to the hurdle signal (inputs to other Adaptrodes). This circuit prevents either response or learning from taking place if the hurdle signal arrives before the x⁰ signal. If x⁰ represents a potential causal event (to be learned) and the hurdle signal results from the effect event, then this circuit prevents association of potential cause with the effect since the former did not precede the latter by some Δ-t. As I show later, this property, along with the temporal encoding scheme described above gives rise to the requisite property of a conditioned learning model that learning goes through a maximum as a function of the interstimulus interval between the onset of the CS (say) and the onset of the UCS.

3.6. MODEL NEURONS AND NEURAL NETWORKS

The conventional formal neuron has a set of input edge weights which are representative of the efficacy of a synapse in contributing to the generation of an action potential by the neuron. Model neurons based on Adaptrodes are not much different except that the single weight (per input) is replaced by an Adaptrode with its internal set of weight signals and its external response. It is the latter which constitutes the input to the spatial integration process leading to an overall activation value for the neuron. Integration is performed once in each time step, the same as the input sample rate, and the resulting activation is compared to a threshold. If the activation exceeds the threshold, then the neuron fires an action potential, otherwise it does not. It is this clocking at the maximum frequency rate which squashes the output signals of neurons to be in the same range as the input signals at the synapses.

Fig. 13.4(b) shows the diagrammatic representation of an Adaptrode-based neuron as compared to Fig. 13.4(a) which shows a "conventional" neuron. The response signals from Adaptrodes, labeled A₁ through A_n, are summed and compared to the threshold, θ, as shown. The output signal, labeled x₀ (where the subscript is used to index neuron signals), will be a 1 (one) if the threshold is exceeded. In Fig. 13.4(b) the output, x₀, serves a second purpose - as input to a special Adaptrode labeled A₀. This Adaptrode may be optionally used for several purposes. One use is to compute a variable threshold based on output signal. This amounts to an activity-dependent learning process at the neuronal level. A second use is to provide a graded response output from the neuron, r₀. This signal may be used to establish cross-neuronal associations as is discussed later.

One major advantage (but also a major problem) gained in constructing neurons with Adaptrodes is the ability to build a wide variety of neuronal types. This is possible because different types of synapses, with different dynamical properties, can be built by designating specific numbers of levels and values of α^k and δ^k for all levels k in that type of Adaptrode. This is an advantage from the standpoint of creating models that emulate real biological neurons. It is problematic from the standpoint of specification. Models that we have built to date have involved no more than three different "types" of neurons and only five different "types" of synapses. Much research is needed to discover a linkage between functional performance and Adaptrode specifications.

Fig. 13.4. Comparison of conventional formal neuron with Adaptrode-based neuron. Adaptrode A₀ provides a local signal proportional to the output rate of the neuron.

A neural network is constructed from a set of neurons, thus defined, an interconnection specification, a set of input slots and a set of output slots. The last two items hold greyscale values. The slot (called inslots or outslots) values are updated several times per model second - we used a 30Hz sample rate. Inslot data comes from an array representing sensory input, say an image file. Outslot data is recorded each frame in a "response" file. There is no imposed architecture, such as layers or "slabs", in the interconnection matrix, though such architectures can easily be constructed.

Within each sample frame (e.g., the 30Hz rate), the neurons are processed over several iterations (with a 30Hz sample rate and a 300Hz pulse rate, this would be 10 iterations per frame). At the start of each iteration a pulse, or lack thereof, is generated for each inslot based on its greyscale. We have used a negative exponential kernel convolution with a white noise component with good results. The pulse is then available as input to any neuron that has an Adaptrode mapped to that slot. No pulse coding is necessary between neurons, however, the injection of some noise seems useful.

Clearly, explicit timing of external signals is a necessary part of simulations using Adaptrode-based neural networks. Phase relations between sensory signals play an important part in simulating conditioned learning tasks. Data sets cannot consist simply of, say, many images to be exposed to the network for one processing cycle. The time order between parts of an image now become important considerations.

4. CONDITIONED RESPONSE MODEL - BASIC ASSOCIATIVE NETWORK

A very simple neural network comprised of two neurons can be used to demonstrate conditioned learning in this model. Fig. 13.5 shows what I call a Basic Associative Network (BAN) that can learn to associate one (or more) uncommitted input signal (conditionable stimulus) with one of several output signals (unconditioned responses), based on its correlation with a matching input signal (unconditionable stimulus). The system can use the uncommitted signal as a predictor of the onset of the unconditionable stimulus, after learning the association, but only if the former reliably precedes the latter in time.

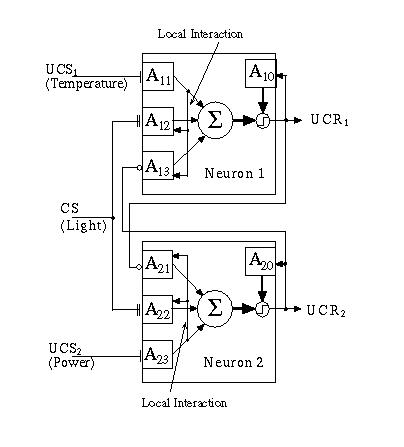
Fig. 13.5. The Basic Associative Network (BAN) is comprised of two neurons which code for different response mechanisms (UCR₁ and UCR₂). External inputs include two unconditionable stimuli (UCS₁ and UCS₂).

Before describing the simulation of the BAN, it is necessary to discuss the manner in which one can instantiate instances of classical learning laws by using Adaptrodes. It turns out that one can construct hurdle set definitions and interconnection matrices that allow one to emulate many of the classical learning laws, such as the Hebb rule. As mentioned above, the use of an output Adaptrode (A₀) in neurons provides a graded response signal which is based on the time-averaged frequency of the pulse-coded neuron output. By feeding this signal back to the hurdle set processor of the "learning", input Adaptrodes, one has potentiation in the latter units, based on the correlation between the input signals at those Adaptrodes and the output signal of the neuron (Fig. 13.6).

Fig. 13.6. An Adaptrode-based neuron using the Hebb rule for learning.

Some workers have suggested that the Hebb rule need not require actual action potential generation from the neuron (Jaffe and Johnston, 1990). Rather they have used the post-synaptic excitatory potential (EPSP) as representing the post-synaptic activity. Thus sub-threshold membrane potentials can be sufficient cause for learning to occur in the contributing synapses. This can be simulated by using the activation signal produced by the neuron integrator (the Σ processor) as feedback to the hurdle sets of the learning Adaptrodes (Fig. 13.7).

Fig. 13.7. A compartmental Hebb rule. The hurdle sets of the learning Adaptrodes include the output of the summation processor. This provides a learning mechanism that does not depend on the actual firing rate of the neuron.

Another learning rule which has been explored by Daniel Alkon (1987; Alkon et al., 1991) and his colleagues is the "local interaction" rule, so called because the signal used to gate weight updates comes not from the neuron output (or activation) but from another, nearby, synapse (input). This latter synapse does not learn but simply provides a strong signal that may activate the neuron. If there is a strong correlation between this "flow-- through" signal and the input signals to nearby modifiable synapses, then the latter are strengthened accordingly. Alkon et al. (1991) produced a working neural network model they call DYSTAL based on this learning rule. Fig. 13.8 shows an Adaptrode-based neuron using the response of one input Adaptrode as the hurdle source for another group of Adaptrodes to simulate a local interaction rule. The reported simulations below, in fact, rely upon this rule.

Fig. 13.8. Local interaction rule. A single input Adaptrode acts to hurdle potentiation in a local cluster of input Adaptrodes.

In spite of the furor over the biological-reality (or lack thereof) of the error backpropagation learning rule (Rumelhart et al., 1985; cf. Crick's comments, 1989), and perhaps more generally of gradient descent processes with their heavy reliance on computational precision, I would not discount the role of error minimization for certain types of learning at a network level in biological systems. With this spirit in mind, I constructed a neural architecture from Adaptrode-based neurons that computes an output error and feeds this signal back to the prior layer of an otherwise feedforward network. Using a form of local interaction rule (as above) and discriminating a Type I (active when it should be quiet) vs. Type II (quiet when it should be active) error one can build a network which fulfills the intent of the delta rule (error minimization-driven learning). By using another neuron to record the time-average values of the total error produced by a single layer in the network, and using the rate of change of this neuron's response, r₀, by using it as a hurdle source for more than one level in the learning Adaptrodes, it is possible to inform a prior layer of its contribution to the overall error. Thereby, the Adaptrodes in this prior layer adjust (potentiate or decay) so as to minimize that contribution. The details are not fully worked out for this architecture, however we simulated small two-layer networks that learn to minimize the error in output (compared with a desired output) in the spirit, though not the method, of backpropagation.

4.1. CLASSICAL CONDITIONING

The two neuron network shown in Fig. 13.5 can be viewed as a simple robot decision controller. The robot, in this case, can sense three environmental conditions, the presence of a power source (i.e., food) at UCS₂, the presence of light at CS, and the presence of high temperature (i.e., pain) at UCS₁. Single flat termini represent non-learning, excitatory inputs, double flat termini represent learning excitatory inputs and circular termini represent non-learning inhibitory inputs. The output of each neuron in the BAN represents an unconditionable response to the corresponding unconditionable input. Thus, a signal at UCS₁ results in an output at UCR₁; values for θ, the threshold, and Κ, the preweighting constant, have been selected to assure that an unconditionable input results in an unconditionable output. An input to the conditionable stimulus alone will not, however, produce a response of significance in either of the two neurons even though it is wired to both of them. This is due, in part, to the slower, and weaker response output from the learning Adaptrodes (A_1,2 and A_2,2). It is also due to the cross inhibition between neurons. Even if a very strong signal at CS is sustained for a period long enough to drive the w0 signals in A_1,2 and A_2,2 high enough to cross their respective thresholds, the cross inhibition between neurons ensures that output from each is inhibited. A signal at CS alone can activate a neuron only if the learning Adaptrode (either A_1,2 or A_2,2) has potentiated to a point that gives w⁰ the ability to climb to a value greater than θ.

A priori, there is no reason to associate light with either pleasure or pain. It is a neutral signal. If, however, there is a causal relationship between the presence of light and the presence of one or the other of the unconditionable stimuli, following the constraints of causality discussed above, then the occurrence of light could be used as a predictor of the occurrence of the UCS. Such a prediction could give the robot a "head start" in reacting to the UCS, which, after all means something important. How then can an association be encoded in the BAN, if a causal relationship exists?

Signals presented to the BAN network are stochastic and noisy (about 10% noise). The input signals are modeled after real neural signal bursts after Richmond, Optican, and Spitzer (1990) convolved with a negative exponential probability density function kernel to generate discrete spikes. After as few as three trials with joint presentation at UCS₂ and CS in the mid-range (representing about 120 Hz peak signals for one-half second, on average, of model time) potentiation occurs in A_2,2 as the result of local interaction between A_2,1 and A_2,2. This potentiation is sufficient so that Neuron 2 will win the competition as a result of input at CS only. Fig. 13.9 shows the relative levels of w⁰ in A_2,2 and A_1,2 at the third episode of stimulation by CS and UCS₂. Since A_1,1 is not active, no potentiation occurs in A_1,2.

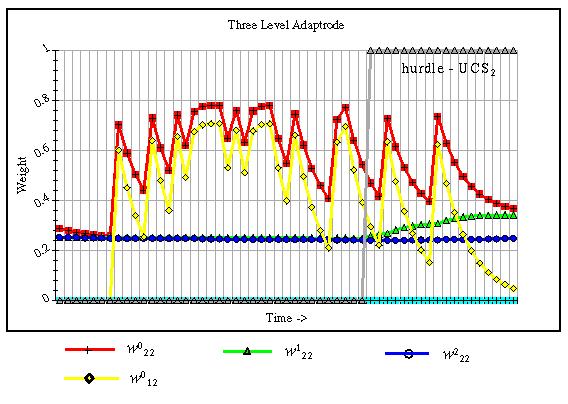
Fig. 13.9. Potentiation comparison between A_2,2 and A_1,2. This graph shows the change in w⁰_2,2, w⁰_1,2, w¹_2,2, and w²_2,2 as a function of the pulsed input and the hurdle signal provided by excitation of UCS₂. w⁰_2,2 starts the episode (third) with an advantage over w⁰_1,2. Toward the end of the episode UCS₂ becomes sufficiently strong so that the response of A_2,1 exceeds the gate threshold of w¹_2,2, thus allowing further potentiation of the latter.

We first condition the network with the CS/UCS₂ pairing for one hundred exposures of 30 to 50 time units and a 100 time unit inter-episode interval (Fig. 13.10). This protocol is clearly artificial and deterministic. More realistic protocols, involving stochastic pairing and variable inter-episode intervals have been simulated. These simulations give the same basic results but extend the simulated time period significantly. After conditioning, the robot will reliably and strongly respond with a seeking behavior when stimulated with a mid-range burst of light (CS) alone.

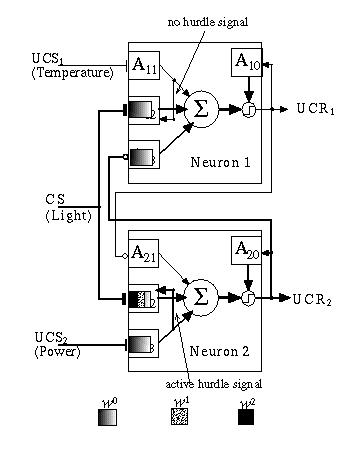
Fig. 13.10. Presentation of CS and UCS₂ signals in proper temporal order leads to potentiation of w²_2,2.

After the network has aged for some period of time without any inputs, Adaptrode A_2,2 maintains a residual memory of the association to which it has been exposed (Fig. 13.11). As a consequence of this residual, the network has established a relationship between the associated signals which can be recalled when a signal is injected at CS only. This corresponds to the robot seeing light alone. Because of the potentiation of A_2,2, the input signal at A_2,2 will more quickly drive w⁰_2,2 to a higher value than is achieved in A_1,2 at w⁰_1,2. In turn, this is enough to drive an output signal at UCR₂ resulting in an inhibitory signal damping the top unit (Fig. 13.12).

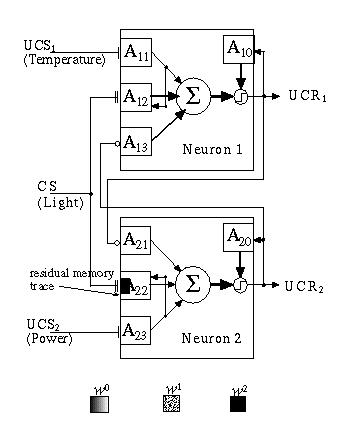
Fig. 13.11. The BAN after aging subsequent to learning an association at A_2,2.

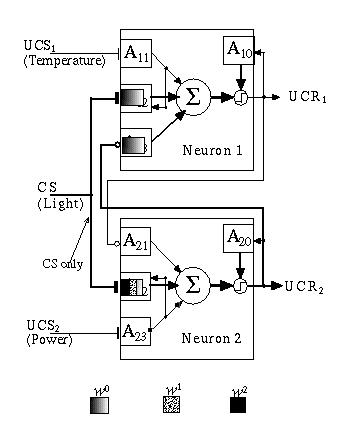
Fig. 13.12. Presentation of CS alone is sufficient to fire a response at UCR₂.

In this way, the network has learned to exploit CS, a non-meaningful signal in its own right, as a predictor of some meaningful signal (in this case power availability). The frequency and intensity with which these two signals occurred together in the past determines the reliability of the predicted association in the future. The robot can learn to seek lights (when it is low on power) and enjoy a certain degree of confidence that the association will be valid in the future.

4.1.1. CONTIGUITY/CONTINGENCY

Contiguity refers to the nearness in time (and generally in space) of the UCS (sometimes called the reinforcer) to the CS. The closer in time a neutral event is to the occurrence of a meaningful event, the stronger the association between these two. In the Adaptrode, a memory trace continually decays toward its equilibrium value after being stimulated. If a hurdle signal is received within a short time after the original priming, the Adaptrode potentiates, or transfers some of the memory trace to a longer-term memory. If the hurdle signal arrives after too long of a delay, then the original trace has decayed beyond a capacity to pull the longer-term weight signal up.

Contingency refers to the correlation between the CS and the UCS. A correlation builds up over time. As was discussed above, if the relative frequency of the co-occurrences of CS with one of the UCSs is higher than that for the other UCS, then an associative encoding between the one with the higher frequency will obtain. In addition, the degree of the correlation depends on the absolute frequency of co-occurrence as opposed to the occurrence of CS alone (without the reinforcer). It should be obvious that the occurrence of the CS alone produces no lasting change in the weight of the Adaptrode.

4.1.2. S-SHAPED ACQUISITION CURVE

One hallmark of conditioned learning is the archetypical rate at which a memory trace is strengthened. Typically, an animal's response rate (the quickness with which it responds to the CS with the UCR) is measured on each trial and this is plotted as a function of number or trials to project a rate of learning curve. The curve is generally shown to be logistic or S-shaped with an initial positively accelerating rate followed by a near-linear period and, finally, a negatively accelerating rate. Such curves have been deemed important evidence of conditioning (Klopf, 1988).

I would generally caution against trying to explain all phenomena with one mechanism and I don't want to be guilty of that here. It seems likely that the logistic rate of memory acquisition may be due to fairly complex network interactions. However, it is intriguing that the encoding rate for the weight signal in the Adaptrode comes closer to approximating a logistic curve as one goes deeper into the structure. Fig. 13.13 shows a graph of the w² level weight during a single episode. At this stage of analysis I can only note the interesting way in which a function, which is locally linear, when embedded in a network such as the Adaptrode, gives rise to nonlinear behavior. This is not unexpected due to the recurrent nature of the Adaptrode. But it is worth noting that the specific form of the nonlinearity is that seen in whole-animal models of memory acquisition. It will be the subject of future research.

Fig. 13.13. w² as a function of time.

[Authors Note: Since subsequent research did show that the apparent S-shaped curve was an artifact of the experimental regime, the above section should be ignored! The graph - Fig. 13.13 is not shown.]

4.1.3. EXTINCTION

Memories, if not reinforced, fade with time. This is true of nonassociative as well as associative memories, requiring an associated reinforcer. In the classical conditioning model, extinction of a memory arises from the presentation of the CS without the reinforcement generated by a following UCS. Presumably, the CS is no longer acting as a good predictor or has come uncoupled causally from the UCS and so should not be retained in association with the latter. A rather large topic of debate has centered around the exact form which extinction takes. That is, it could be due to simple passive decay (or forgetting), it could be due to active decay (selective forgetting - Grossberg, 1991), or as was originally suggested by Pavlov (1927), it could be due to active inhibition. Different opinions on the exact nature of the underlying mechanism abound.

As stated above, it is probably dangerous to infer mechanisms from observations of the whole-animal model to the cellular substrates (and neural network models). It would be desirable to correspond performance observations in simple invertebrate systems such as Aplysia (Small et al., 1989) or Hermissenda (Alkon, 1987) with those in birds and mammals, in order to make such inferences.

In the Adaptrode model, as presented here, the nature of reduction of an effective weight (the response of the Adaptrode) is through passive decay, but one which is proportional to the distance the weight is above equilibrium. However, this is accomplished in a piecewise fashion across multiple time scales. Thus over short time frames, say a series of trials with short inter-episode periods, followed by presentation of the CS only, there would appear to be a rapid decay of the efficacy weight giving the impression of active decay. Over longer time frame protocols, the extinction curve starts to look passive. This is, in fact, what we have seen in simulations. As is discussed below, in the case of learning a new, contrary association, we even see a curve which appears to be due to active decay. These findings suggest that the appearance of passive vs. active decay may be influenced strongly by the temporal nature of the protocol used. This is certainly a testable idea. We have not seen, nor specifically have we looked for, evidence of completely selective forgetting. I suspect that some form of selective forgetting is emergent at the neuronal network level as opposed to the synaptic level of organization.

An interesting aspect of passive decay of long-term memory in the Adaptrode is that the effective weight can decay below the threshold necessary for the single Adaptrode to initiate a neuron output. The memory appears, from the outside to have decayed away.

However, because there is a long-term trace remaining, a new series of CS-UCS co-presentations causes reacquisition in a fewer number of trials which is not unlike what occurs in animal models.

4.2. SECONDARY CONDITIONING

Following the protocol given above (statistically significant pairings of CS followed by a UCS) the CS becomes able to initiate the UCR by itself. This is generally referred to as primary conditioning. Secondary conditioning comes from the pairing of a second CS with a following CS that has already been conditioned to predict the UCS (i.e., produce the UCR). Using the compartmental Hebbian rule (Fig. 13.7), we simulated this phenomenon. One compartment, in this model, comprises one UCS input and two or more CS inputs. After training the system on a particular CS-UCS pairing which produced a deep, sustained encoding, we then paired the trained CS, call it CS₁, with another CS input, call it CS₂. The latter successfully became a predictor of the former, and that, in turn remained a predictor of the UCS.

If presentations of the CS signals alone were not occasionally followed by reinforcement from the UCS, then both memory traces extinguished in the reverse order. That is, CS₂ extinguished first followed by CS₁.

4.3. BLOCKING

An interesting phenomenon occurs when a second CS is correlated with the UCS in the same temporal frame as the first CS but for which the first CS has already encoded the association. In this case, the existence of a CS₁-UCR coding blocks the encoding of the second CS, CS₂, from becoming associated with the UCS-UCR. Since a predictor of the UCS already exists, there is presumably no need for a second predictor having the same temporal relation so it is effectively ignored.

It turns out that the same mechanism that gives rise to secondary conditioning is involved in blocking, namely the compartmental Hebbian rule. The actual blocking, however, is due to the gating of input signal to the Adaptrode via the circuit shown in Fig. 13.3. The arrival of a hurdle signal prior to the buildup of a response signal prevents the input signal at x⁰ from entering the Adaptrode, thus preventing any growth of w⁰ and any run-away effect on potentiation.

4.4. INTERSTIMULUS INTERVAL (ISI) EFFECTS

The window of opportunity for encoding is enforced such that there is an optimum period between the onset of the CS and the onset of the UCS during which the memory strength will be maximum. If the UCS starts too soon after the onset of the CS, then recording will be minimal. If the UCS starts too late after the offset of the CS, then, likewise, recording will be minimum. A plot of recording strength of the memory vs. the interstimulus interval (ISI) shows an inverted U shape as efficacy rises to a maximum then falls off (Grossberg, 1991).

Fig. 13.14 shows a graph of the level of w² in an Adaptrode. The time axis shows the number of time increments between the onset of the CS (x⁰) and the onset of the UCS (hurdle signal). A short burst of five pulses was used as the CS. The hurdle signal was turned on for 10 pulses. No attempt was made to replicate biological conditions (a typical optimum ISI is 0.5 sec. - Klopf, 1988). The curve as shown is only qualitatively similar to the effect in conditioned learning examples.

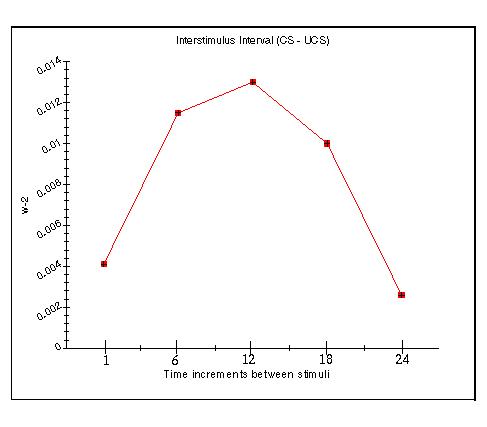
Fig. 13.14. The level of w² as a function of ISI.

The inverted U comes about due to the enforcement of the CS-first rule at the front end (short ISI) and the rapid decay of w⁰ and w¹ after the offset of the CS at the tail end (long ISI).

4.5. NON-INTERFERING, MUTUALLY EXCLUSIVE ASSOCIATIONS

Now we address a new and more difficult consideration, one which depends on the multi-time domain encoding capabilities of the Adaptrode.

Suppose that, after primary conditioning as described in Section 4.1, for some short interval of time a contrary relationship exists between UCS1 and CS as, for example, might happen if a fire were to break out in the robot's environment. First, we would be concerned with the appropriate response - that is, the robot should avoid the fire. Second, we need some means of determining the significance of this contrary condition. Is it just noise or does it represent a more permanent change in the nature of the environment? Third, in the event that this new relationship is temporary (as compared to the duration of the prior conditioning), we certainly don't want the robot to forget the prior association since there is some possibility that the old relationship will again be the norm in the future.

In this experiment the network is exposed to a single high frequency exposure to UCS₁ and CS for 100 time units (Fig. 13.15). This situation is clearly contrary to the system's prior conditioning. The system initially starts to fire the neuron in which the long-term association is encoded as if responding to the availability of power. It takes a small amount of time (approximately 20 time units) for the w⁰ value of A_1,1 to build to a level sufficient to override, through the inhibitory link at A_2,1, the output of this neuron. However, due to the more rigorous firing of the UCS₁/UCR₁ neuron, the latter wins the competition leading to the appropriate response (avoidance) at UCR₁. Note that, due to the relative lengths of time of exposures to the two different conditions, A_2,2 potentiates to w² level while A_1,2 is potentiated only to w¹.

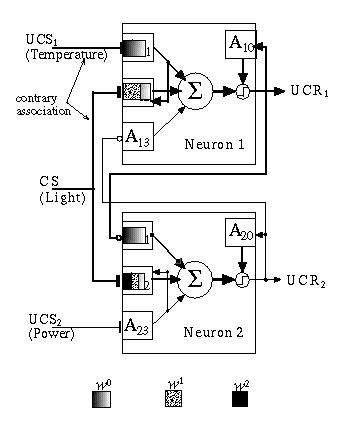
Fig. 13.15. A short but intense, contrary association between UCS1 and CS leads to some potentiation of w² in A_1,2, but little potentiation of w³. The combined inputs at A_1,1 and A_1,2 are sufficient to fire neuron 1 and damp out a response from neuron 2.

If the network is now presented with the CS input only (Fig. 13.16), it will, for a short while, respond, if only weakly, with output at UCR₁. The reason is that w¹_1,2 has risen to a level just slightly greater than that of w¹_2,2. This will persist until w¹_1,2 has decayed to the same level as w¹_2,2 at which time the response will be ambiguous. The ambiguity will not last for long. Since the exposure to the contrary condition was short, compared with the "normal" association, and w²_1,2 did not rise significantly, w¹_1,2 continues to decay, falling below the level of w¹_2,2. At that time, approximately 300 time units after the contrary conditioning, the network responds with the original UCR₂ response as the older association reemerges as dominant (Fig. 13.17).

Fig. 13.16. Short-term learning of the contrary association causes output at UCR₁ on presentation of CS alone, shortly after the learning occurred.

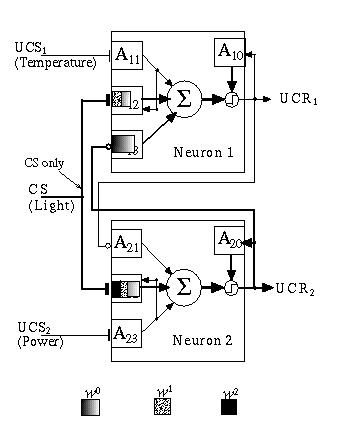
Fig. 13.17. The older association between CS and UCS₂/UCR₂ emerges after potentiation of w² at A_2,2 decays below the w³ level of A_1,2.

This network, then, has the capacity to encode contrary associations which separate in time as opposed to space. The memory traces can be maintained without interference. If the short-term, newly encoded association is actually caused by a new causal alignment in the environment, then it will be reinforced and eventually completely override the former memory. If, on the other hand, the environment returns to the alignment which gave rise to the former encoding, the older memory will reemerge. It will be strengthened (in essentially the manner of reacquisition) by the old reinforcement while the newer trace will decay.

5. CONCLUSIONS AND FUTURE DIRECTIONS

The Adaptrode model has a number of features in common with many of the recurrent models of neural networks. The main difference is that here the recurrent activations, representing memory of prior activations, are brought down to the level of the synapse rather than operating at the level of the network. This allowed us to concentrate on the memory encoding of single channels, capturing the temporal behavior of a signal first. The establishment of associations between signals, both spatial and temporal, is achieved secondarily.

In this chapter I put forth the notion that neuronal systems that show conditioned learning abilities meet the constraints of causal inference and could thereby be viewed as a fundamental mechanism for higher-level architectures that capture the cognitive flavor of causality. It is not a question of whether the conditionable causes the unconditionable stimulus (or even that the cause of the former is the cause of the latter). Rather, it is the fact that causal relationships, indeed causal chains, can be inferred from the temporal relationships allowed by conditioned learning. The inference of causality confers an evolutionarily useful ability on its possessor. It allows an animal to predict the future with respect to the occurrence of events that have direct physiological, and/or survival consequences from those that are essentially neutral.

A framework for investigation of higher-level cognitive processes begins to emerge. The synaptic and neuronal substrates of conditioned learning wherein specific temporal constraints on the relationship between two events is being established. The encoded temporal relationship of conditioned learning has the same form as a causal relationship, namely one event, the cause, must precede the other event, the effect, within a temporal window of opportunity. Furthermore, mechanisms such as secondary conditioning may be invoked as a basis for encoding causal chains.

It is a far leap from conditioned learning, say in Hermissenda crassicornis (Alkon, 1987), to the cognitive ability, in humans, to infer causality from observations of the environment. The idea that a relatively simple neural mechanism can provide a means for encoding the temporal relationships involved in causality is, however, intriguing. The capacity of the Adaptrode model, to encode the temporal aspects of conditioned learning may provide a useful modeling tool for investigation of higher-order cognitive processes.

Investigations of Adaptrode-based neural networks are just getting underway. We are currently developing neural networks for pattern recognition and categorization as well as models of operant conditioning and adaptive control. A network compiler is being built to allow the construction of very large networks (over 100 neurons and hundreds of thousands of connections). A runtime engine (written in C) is already being used in our lab to run simulations of small network models such as those reported above. Once the compiler is completed we will begin investigating larger-scale learning dynamics.

REFERENCES

• Alkon, D. L. (1987). Memory Traces in the Brain. New York: Cambridge University Press.
  
• Alkon, D. L. (1989). Memory storage and neural systems. Scientific American, July, Vol. 261, No. 1, pp. 42-50.
  
• Alkon, D. L., Blackwell, K. T., Barbour, G. S., Rigler, A. K., and Vogl, T. P. (1990). Pattern-recognition by an artificial network derived from biologic neuronal systems. Biological Cybernetics 62, 363-376.
  
• Alkon, D. L., Vogl, T. P., Blackwell, K. T., and Tam, D. (1991). Memory function in neural and artificial networks. In M. L. Commons, S. Grossberg, and J. E. R. Staddon, (Eds.), Neural Network Models of Conditioning and Action (pp. 1-11). Hillsdale, NJ: Lawrence Erlbaum Associates.
  
• Anderson, S., Merrill, J. W. L., and Port, R. (1989). Dynamic speech categorization with recurrent networks. In D. Touretzky, G. E. Hinton, and T. J. Sejnowski (Eds.), Proceedings of the 1988 Connectionist Models Summer School (Pittsburgh, 1988) (pp. 398-406). San Mateo, CA: Morgan Kaufmann.
  
• Aparicio, M., IV (1988). Neural computations for true Pavlovian conditioning: control of horizontal propagation by conditioned and unconditioned reflexes. Unpublished doctoral disserta- tion. University of South Florida.
  
• Buonomano, D. V., Baxter, D. A., and Byrne, J. H. (1990). Small networks of empirically derived adaptive elements simulate some higher-order features of classical conditioning. Neural Networks 3, 507-523.
  
• Byrne, J. H., and Gingrich, K. J. (1989). Mathematical model of cellular and molecular processes contributing to associative and nonassociative learning in Aplysia. In J. H. Byrne and W. O. Berry (Eds.), Neural Models of Plasticity (pp. 58-72). Orlando: Academic Press.
  
• Byrne, J. H., Gingrich, K. J., and Baxter, D. A. (1990). Computational capabilities of single neurons relationship to simple forms of associative and nonassociative learning in Aplysia. In R. D. Hawkins and G. H. Bower (Eds.), Computational Models of Learning (Vol. 23: Psychology of Learning and Motivation (pp. 31-63). New York: Academic Press.
  
• Carpenter, G. A., and Grossberg, S. (1987a). A massively parallel architecture for a self-organizing neural pattern recognition machine. Computer Vision, Graphics, and Image Processing 37, 54-115.
  
• Carpenter, G. A., and Grossberg, S. (1987b). ART2: Self-organization of stable category recognition codes for analog input patterns. Applied Optics 26, 4919-4930.
  
• Crick, F. (1989). The recent excitement about neural networks. Nature 337, 129-32.
  
• Dretske, F. I. (1988). Explaining Behavior: Reasons in a World of Causes. Cambridge, MA: MIT Press.
  
• Elman, J. L. (1990). Finding structure in time. Cognitive Science 14, 170-211.
  
• Elman, J. L., and Zipser, D. (1988). Discovering the hidden structure of speech. Journal of the Acoustical Society of America 83, 1615-1626.
  
• Gelperin, A., Hopfield, J. J., and Tank, D. W. (1985). The logic of Limax learning. In A. I. Selverston (Ed.), Model Neural Networks and Behavior (pp. 237-261). New York: Plenum.
  
• Getting, P. A. (1980). Emerging principles governing the operation of neural networks. Annual Review of Neuroscience 12, 185-204.
  
• Grossberg, S. (1982). Studies of Mind and Brain: Neural Principles of Learning, Perception, Development, Cognition, and Motor Control. Boston: Reidel Press.
  
• Grossberg, S. (1987). Competitive learning: From interactive activation to adaptive resonance. Cognitive Science 11, 23-63.
  
• Grossberg, S. (1991). A neural network architecture for Pavlovian conditioning: reinforcement, attention, forgetting, timing. In M. L. Commons, S. Grossberg and J. E. R. Staddon, (Eds.), Neural Network Models of Conditioning and Action (pp. 1-11). Hillsdale, NJ: Lawrence Erlbaum Associates.
  
• Hebb, D. O. (1949). The Organization of Behavior. New York: Wiley.
  
• Hertz, J., Krogh, A., and Palmer, R. G. (1991). Introduction to the Theory of Neural Computation. Santa Fe Institute Studies in the Sciences of Complexity. Reading, MA: Addison-Wesley.
  
• Jaffe, D., and Johnston, D. (1990). Induction of long-term potentiation at hippocampal mossy-fiber synapses follows a Hebbian rule. Journal of Neurophysiology 64, 948-960.
  
• Kandel, E. R., and Schwartz, J. H. (1982). Molecular biology of learning: Modulation of transmitter release. Science 218, 433-443.
  
• Klopf, A. H. (1988). A neuronal model of classical conditioning. Psychobiology, 16, 85-125.
  
• Klopf, A. H. and Morgan, J. S. (1990). The role of time in natural intelligence implications of classical and instrumental conditioning for neuronal and neural network modeling. In M. Gabriel and J. Moore (Eds.), Learning and Computational Neuroscience (pp. 463-495). Cambridge, MA: MIT Press.
  
• Koch, C., and Segev, I. (1989). Introduction. In C. Koch and I. Segev (Eds.), Methods in Neuronal Modeling: From Synapses to Networks (pp. 1-8). Cambridge, MA: MIT Press.
  
• Kosko, B. (1986). Differential Hebbian learning. In J. S. Denker (Ed.), AIP Conference Proceedings 151: Neural Networks for Computing (pp. 277-282). New York: American Institute of Physics.
  
• Mackintosh, N. J. (1983). Conditioning and Associative Learning. Oxford: Oxford University Press.
  
• Mobus, G. E. (1990). The adaptrode learning model: applications in neural network computing. Tech. Rep. No. CRPDC-90-5, Center for Parallel and Distributed Computing, University of North Texas, Denton.
  
• Mobus, G. E., and Fisher, P. S. (1990). An adaptive controller using an adaptrode-based artificial neural network. Tech. Rep. No. CRPDC-90-6, Center for Parallel and Distributed Computing, University of North Texas, Denton.
  
• Mobus, G. E., Cherri, M., and Fisher, P. S. (1993). The Adaptrode: Part I. Temporal, nonassociative reinforcement learning in multiple time domains. Manuscript submitted for publication.
  
• Morgan, J. S., Patterson, E. C. and Klopf, A. H. (1990). Drive-reinforcement learning: a self-supervised model for adaptive control. Network 1, 439-448.
  
• Pavlov, I. P. (1927). Conditioned Reflexes (V. Anrep, trans.). London: Oxford University Press.
  
• Richmond, B. J., Optican, L. M., and Spitzer, H. (1990). Temporal encoding of two-dimensional patterns by single units in primate primary visual cortex. I. Stimulus-response relations. Journal of Neurophysiology 64, 351-369.
  
• Rumelhart, D. E., Hinton, G. E., and Williams, R. J. (1985). Learning internal representations by error propagation. ICS Report 8506. Institute of Cognitive Science, University of California, San Diego.
  
• Rumelhart, D. E., and McClelland, J. L. (Eds.) (1986). Parallel Distributed Processing: Explorations in the Microstructure of Cognition, Vols. 1 and 2. Cambridge, MA: MIT Press.
  
• Sejnowski, T. J., Chattarji, S. and Stanton, P. (1989). Induction of synaptic plasticity by Hebbian covariance in the hippocampus. In R. Durbin, C. Miall, and G. Mitchison (Eds.) The Computing Neuron (pp. 105-124). Reading, MA: Addison-Wesley.
  
• Small, S. A., Kandel, E. R., and Hawkins, R. D. (1989). Activity-dependent enhancement of presynaptic inhibition in Aplysia sensory neurons. Science 243, 1603-1605.
  
• Staddon, J. E. R., and Zhang, Y. (1991). On the assignment-of-credit problem in operant learning. In M. L. Commons, S. Grossberg, and J. E. R. Staddon (Eds.), Neural Network Models of Conditioning and Action (pp. 279-293). Hillsdale, NJ: Lawrence Erlbaum Associates.
  
• Starmer, C. F. (1987). Characterizing synaptic plasticity with an activity dependent model. In M. Caudill and C. Butler (Eds.), Proceedings of the IEEE First International Conference on Neural Networks (Vol. IV, pp. 3-10). San Diego: IEEE/ICNN.
  
• Sutton, R. S. (1988). Learning to predict by the methods of temporal differences. Machine Learning 3, 9-44.
  
• Sutton, R. S., and Barto, A. G. (1987). A temporal-difference model of classical conditioning. Tech. Rep. No. 87-509.2. Waltham, MA: GTE Laboratories.
  
• Sutton, R. S. and Barto, A. G. (1990). Time derivative models of Pavlovian reinforcement. In M. Gabriel, M. and J. Moore (Eds), Learning and Computational Neuroscience (pp. 463-495). Cambridge, MA: MIT Press.
  
• Tesauro, G. (1986). Simple neural models of classical conditioning. Biological Cybernetics 55, 187-200.
  
• Widrow, B., and Hoff, M.E. (1960). Adaptive switching circuits. In 1960 IRE WESCON Convention Record (part 4, pp. 96-104). New York: IRE.