We also show how the simulation envelop is constructed that is frequently used to describe whether a measured pattern departs from an expected distribution. The values for the distance statistic, tyically K(d) [or its transform L(d)], or G(d) are calculated for the observed pattern and then compared against the statistic calculated for simulated patterns. Typically 99 patterns are used so that if the observed pattern is judged to differ from them all then the pattern is judged as different by 1 in 100. The way this has been done is to calculate a simulation envelop, shown to the right.
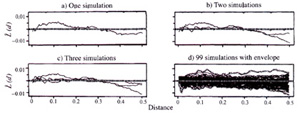
Generating a Monte Carlo envelope for Lˆ (d ). (a) One simulation of complete spatial randomness (CSR) for n points. (b) A second simulation of CSR for n points added to the first simulation. (c) A third simulation of CSR for n points added. (d) Ninety-nine simulations of CSR and the resulting Monte Carlo envelope (stippled line) which is taken as the maximum and minimum values encountered at all distances.
- This method for maing inference is invalid because it violates the assumptions of Monte Carlo methods and results in incorrect type I error rate performance.
- Ecologists' sometimes attempt to identify the scale of deviation from randomness by observing at what distance a data calculation cuts the envelop. However, K(d) and G(d) are cummulative distributions (even where the L transformation is used) so that the value at any distance is determined by the values of lesser (d).
- The use of a random distribution as a test for a spatial pattern is uniformative. Sufficient examinations have been made that deviation from random is the expected situation and a more informative null model is needed.
 Lattice statistics
Lattice statistics