Model Assessment

Model Asessment

Assessment is an important problem in ecological modeling.   Many models have been written but we can have difficulty in judging their effectiveness, both absolutely in relation to particular data and relatively when we come to compare models.   These problem were brought home to us when Kristen Sorrensen-Cothern examined a model    (WHORL) she had written for branch growth and canopy competition.   She found that different combinations of parameter values gave very similar results and it was not clear why this should be so, nor how we could use the model, which was our integration of how we thought the process functioned, to draw conclusions.   We have followed two lines of research to solve this problem.

The first has been to establish a method for calculating how a model may simulate different combinations of outputs effectively by calculating the Pareto optimal set of outputs.  Although a modeller may be most interested in one particular output from a model as a model becomes more complex and contains more parameters there is increasing possibility that parameter values may compensate for inadequacies in the structure of the model, this can produce the problems of "over parameterization" and accommadation, where parameters can take values tp compensate for deficiencies in model structure. A technique is to attempt to get the model to simultaneously simmulate a number of criteria.

The second has been to use this first method to assess the underlying theory on which the model is based.

Pareto optimality

Joel Reynolds continued work on WHORL and looked at its ability to simulate 10 output criteria that were measures of population and crown growth and structure.   Limits, based on measured values, were set for these criteria and WHORL was only able to achieve specific combinations of these criteria and not all of them simultaneously.   The full set of achieved combinations of assessment criteria is the Pareto optimal set.   The parameter values that achieve these different combinations give indication of how the model functions.   The Pareto optimal set is calculated using an evolutionary algorithm that iteratively combines different parameter values and, by changing parameter values, "mutation", and exchanging them between different sets of parameters, "cross-over", evolves towards a solution.   The program for this calculation, and a manual, can be obtained at Joel Reynolds' web site under ParetoEvolve.

A further example is the analysis of hourly increments of conifer shoot growth using a model of environmental variables by Rie Komuro.

In both examples the model was improved and choices of assessment criteria were developed as model assessment took place.

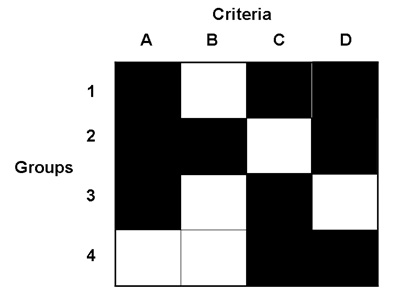
Illustration of a set of assessment vectors where four criteria, A, B, C and D, are not satisfied by any one group. Satisfied criteria are represented by black squares, unsatisfied criteria by white squares. A group contains at least one parameterization of the model that achieves all of the criteria marked as black squares. Individuals in groups 1 and 2 both achieve three criteria and are non-dominated but those in group 3 and group 4 are both dominated by group 1. Some parameterizations of the model may not achieve a unique group of criteria and are considered as "dominated" by those that do and are discarded from further consideration. The evolutionary computation algorithm continually attempts to produce groups that achieve more combinations of assessment criteria.

Assesing the theory underlying models

We have used the construction of Pareto optimal sets to explore uncertainty in ecological theories. We show how uncertainty in a model can be reduced by challenging the theory that underlies it and show how a model can predict different outcomes and so provided indication of how the processes producing them can have some common features. In both examples the distribution of parameter values is studied as well as the Pareto optimal set of assessment criteria.

In  Turley &Ford (2009) we define uncertainty in ecological process models and how it should be calculated. We identify two components of ecological theories: non-uniqueness and incomplete specification.

Non-uniqueness is the characteristic that there may be alternative representations of a theory, or some part of it, and no a priori way of deciding between them. It occurs because, during theory construction, choices are made about processes to include and how these processes will be represented.

When a theory is constructed it may explain some, but not all, of the observed features of a phenomenon and in this sense the theory is incompletly specified. This may happen when there is concentration on some supposed main effect. Scientists are likely to debate which among a set of criteria is central to understanding a process�but the contention here is that a model that simulates a number of criteria effectively is likely to be more completely specified particularly if some of the criteria test details of model functioning.

Assessment criteria: Uncertainty in a process model is reduced as the model can simultaneously simulate an increased number of assessment criteria selected to test specific aspects of the theory being investigated, and within acceptable limits set for those criteria. This reduces incomplete specification of the model. The calculation required is computation of the Pareto set. The definition it provides is the list of simultaneously achieved criteria within specified ranges.
Parameter values: Uncertainty in a process model is reduced as the distribution of values for parameters simulating multiple assessment criteria within their acceptable limits becomes unimodal and with reduced range. This reduces non-uniqueness in the model. The calculation required is analysis of parameter values within each group of the Pareto set, for their distributions and possible correlations. This contributes to a definition of non-uniqueness in terms of whether multiple modes in parameter values are equally plausible. It can also provide understanding of how a model may accommodate to some data.

Kennedy et al. (2010) show that the use of multiple criteria is a powerful tool to explain variability in optimal behavior when the relative contributions of the criteria to overall plant performance are unknown. Many hypotheses have been advanced about factors that control tree longevity. We use a simulation model with multi-criteria optimization and Pareto optimality to determine branch morphologies in the Pinaceae that minimize the effect of growth limitations due to water stress while simultaneously maximizing carbohydrate gain. Two distinct branch morphologies
in the Pareto optimal space resemble Pseudotsuga menziesii (Mirb.) Franco and Abies grandis (Dougl. ex D. Don) Lindl., respectively. These morphologies are distinguished by their performance with respect to two pathways of compensation for hydraulic limitation: minimizing the mean path length to terminal foliage (Pseudotsuga) and minimizing the mean number of junction constrictions to terminal foliage (Abies). Within these two groups, we find tradeoffs between the criteria for foliage display and the criteria for hydraulic functioning, which shows that an appropriate framework for considering tree longevity is how trees compensate, simultaneously, for multiple stresses. The diverse morphologies that are found in a typical old-growth conifer forest may achieve compensation in different ways. The method of Pareto optimization that we employ preserves all solutions that are successful in achieving different combinations of criteria.