Thus far, we have focused on universal issues in user interface design and implementation. This chapter will be the first in which we discuss specific paradigms of interaction and the specific theory that underlies them. Our first topic will be  pointing .

What is pointing?

Fingers can be pretty handy (pun intended). When able, we use them to grasp nearly everything. We use them to communicate through signs and gesture. And at a surprisingly frequent rate each day, we use them to  point , in order to indicate, as precisely as we can, the identity of something (that person, that table, this picture, those flowers). As a nearly universal form of non-verbal communication, it’s not surprising then that pointing has been such a powerful paradigm of interaction with user interfaces (that icon, that button, this text, etc.).

Pointing is not strictly related to interface design. In fact, back in the early 1950s, Paul M. Fitts was very interested in modeling human performance of pointing. He began developing predictive models about pointing in order to help design dashboards, cockpits, and other industrial designs for manufacturing. His focus was on “aimed” movements, in which a person has a  target  they want to indicate and must move their pointing device (originally, their hand) to indicate that target. This kind of pointing is an example of a “closed loop” motion, in which a system (e.g., the human) can react to its evolving state (e.g., here the human’s finger is in space relative to its target). A person’s reaction is the continuous correction of their trajectory as they move toward a target. Fitts began measuring this closed loop movement toward targets, searching for a pattern that fit the data, and eventually found this law, which we call  Fitts’ Law :

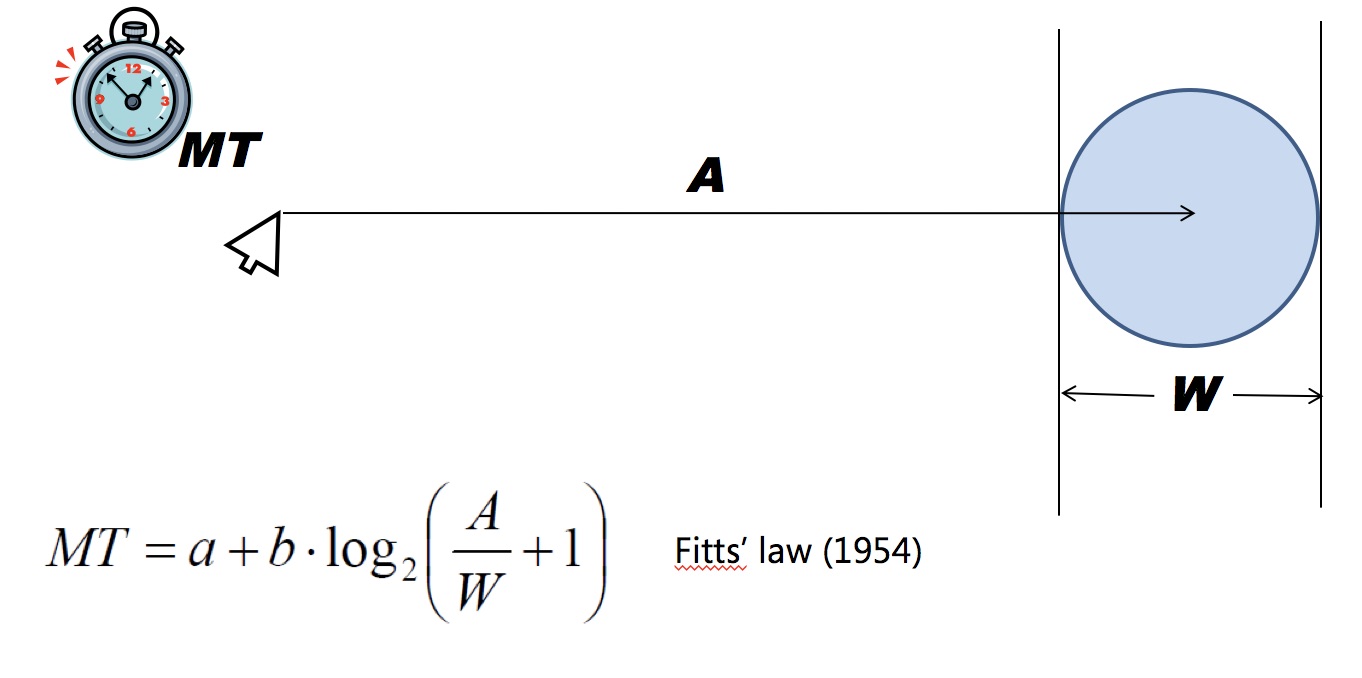
Let’s deconstruct this equation:

• The formula computes the time to reach a target ( MT  refers to “motion time”). This is, simply, the amount of time it would take for a person to move their pointer (e.g., finger, stylus) to precisely indicate a target. Computing this time is the goal of Fitt’s law, as it allows us to take some set of design considerations and make a prediction about pointing speed.
• The  A  in the figure is how far one must move to reach the target (e.g. how far your finger has to move from where it is to reach a target on your phone’s touch screen. Imagine, for example, moving your hand to point to an icon on your smartphone; that’s a small  A . Now, imagine moving a mouse cursor on a wall-sized display from one side to the next. That would be a  large   A . The intuition behind accounting for the distance is that the larger the distance one must move to point, the longer it will take.
• The  W  is the size (or “width”) of the target. For example, this might be the physical length of an icon on your smartphone’s user interface, or the length of the wall in the example above. The units on these two measures don’t really matter as long as they’re the same, because the formula above computes the ratio between the two, canceling the units out. The intuition behind accounting for the size of the target is that the larger the target, the easier it is to point to (and the smaller the target, the harder it will be).
• The  a  coefficient is a user- and device-specific constant. It is some fixed constant minimum time to move; for example, this might be the time it takes for your desire to move your hand results in your hand actually starting to move, or any lag between moving a computer mouse and the movement starting on the computer.  The movement time is therefore, at a minimum,  a . This varies by person and device, accounting for things like reflexes and latency in devices.
• The  b  coefficient is a measure of how efficiently movement occurs. Imagine, for example, a computer mouse that weighs 5 pounds; that might be a large  b , making movement time slower. A smaller  b  might be something like using eye gaze in a virtual reality setting, which requires very little energy. This also varies by person and device, accounting for things like user strength and the computational efficiency of a digital pointing device.

This video illustrates some of these concepts visually:

So what does the formula  mean ? Let’s play with the algebra. When  A  (distance to target) goes up, time to reach the target increases. That makes sense, right? If you’re using a touch screen and your finger is far from the target, it will take longer to reach the target. What about  W  (size of target)? When that goes up, the movement time goes  down . That also makes sense, because easier targets (e.g., bigger icons) are easier to reach. If  a  goes up, the minimum movement time will go up. Finally, if  b  goes up, movement time will also increase, because movements are less efficient. The design implications of this are quite simple: if you want fast pointing, make sure 1) the target is close, 2) the target is big, 3) the minimum movement time is small, and 4) movement is efficient.

There is one critical detail missing from Fitt’s law: errors. You may have the experience, for example, of moving a mouse cursor to a target and missing it, or trying to tap on an icon on a touch screen, and missing it. These types of pointing “errors” are just as important is movement time, because if we make a mistake, we may have to do the movement all over again. Wobbrock et al. considered this gap and found that Fitts’ law itself actually strongly implies a speed accuracy tradeoff: the faster one moves during pointing, the less likely one is to successfully reach a target. However, they also showed experimentally that the particular error rates are more sensitive to some factors than others:  a  and  b  strongly influence error rates, and to a lesser extent, target size  W  matters more than target distance  A ^{16 16}

Jacob O. Wobbrock, Edward Cutrell, Susumu Harada, and I. Scott MacKenzie (2008). An error model for pointing based on Fitts' law. ACM SIGCHI Conference on Human Factors in Computing Systems (CHI).

What does pointing have to do with user interfaces?

But there are some other interesting implications for user interface design in the algebraic extremes. For example, what if the target size is  infinite ? An example of this is the command menu in Apple Mac OS applications, which is always placed at the very top of a screen. The target in this case is the top of the screen, which is effectively infinite in size, because no matter how far past the top of the screen you point with a mouse, the operating system always constrains the mouse position to be within the screen boundaries. This makes the top of the screen (and really any side of the screen) a target of infinite size. A similar example is the Windows Start button, anchored to the corner of the screen. And according to Fitts’ Law, these infinite target sizes means effectively zero movement time. That’s why it’s so quick to reach the menu on Mac OS and the Start button on Windows: you can’t miss.

What’s surprising about Fitts’ Law is that, as far as we know, it applies to any kind of pointing: using a mouse, using a touch screen, using a trackball, using a trackpad, or reaching for an object in the physical world. That’s conceptually powerful because it means that you can use the idea of large targets and short distance to design interfaces that are efficient to use. As a mathematical model used for prediction, it’s less powerful: to really predict exactly how long a motion will take, you’d need to estimate a distribution of those  a  and  b  coefficients for a large group of possible users and devices. Researchers carefully studying motion might use it to do precise modeling, but for designers, the concepts it uses are more important.

Now that we have Fitts’ law as a conceptual foundation for design, let’s consider some concrete design ideas for pointing in interfaces. There are so many kinds: mice, styluses, touch screens, touch pads, joysticks, trackballs, and many other devices. Some of these devices are  direct pointingdirect pointing: Pointing devices in which the input for pointing and the corresponding feedback in response occur in the same physical place (e.g., a touchscreen).  devices (e.g., touch screens), in which input and output occur in the same physical place (e.g., a screen or some other surface). In contrast,  indirect pointingindirect pointing: Pointing devices in which the input for pointing and the corresponding feedback in response occur in different physical places (e.g., a mouse and a screen).  devices (e.g., a mouse, a touchpad, a trackball) provide input in a different physical place from where output occurs (e.g., input on a device, output on a non-interactive screen). Each has their limitations: direct pointing can result in  occlusion  where a person’s hand obscures output, and indirect pointing requires a person to attend to two different places.

There’s also a difference between  absoluteabsolute pointing: Pointing devices in which the physical coordinates of input are mapped directly onto the interface coordinate system (e.g., touchscreens).  and  relativerelative pointing: Pointing devices in which changes in the physical coordinates of input device are mapped directly  changes  to the current position in an interface coordinate system (e.g., mice).  pointing. Absolute pointing includes input devices where the physical coordinate space of input is mapped directly onto the coordinate space in the interface. This is how touch screens work (bottom left of the touch screen is bottom left of the interface). In contrast, relative pointing maps  changes  in a person’s pointing to changes in the interface’s coordinate space. For example, moving a mouse left an inch is translated to moving a virtual cursor some number of pixels left. That’s true regardless of where the mouse is in physical space. Relative pointing allows for variable  gain , meaning that mouse cursors can move faster or slower depending on a user’s preferences. In contrast, absolute pointing cannot have variable gain, since the speed of interface motion is tied to the speed of a user’s physical motion.

How can we make pointing better?

When you think about these two dimensions from a Fitts’ law perspective, making input more efficient is partly about inventing input devices that minimize the  a  and  b  coefficients. For example, researchers have invented new kinds of mice that have multi-touch on them, allowing users to more easily provide input during pointing movements ^{15 15}

Nicolas Villar, Shahram Izadi, Dan Rosenfeld, Hrvoje Benko, John Helmes, Jonathan Westhues, Steve Hodges, Eyal Ofek, Alex Butler, Xiang Cao, Billy Chen (2009). Mouse 2.0: multi-touch meets the mouse. ACM Symposium on User Interface Software and Technology (UIST).

Other innovations focus on software, and aim to increase target size or reduce travel distance. Many of these ideas are  target-agnostic  approaches that have no awareness about what a user might be pointing  to . Some target-agnostic techniques include things like mouse pointer acceleration, which is a feature that makes the pointer move faster if it determines the user is trying to travel a large distance ^{3 3}

Casiez, G., Vogel, D., Balakrishnan, R., & Cockburn, A. (2008). The impact of control-display gain on user performance in pointing tasks. Human-Computer Interaction.

Other pointing innovations are  target-aware , in that the technique needs to know the location of things that a user might be pointing to so that it can adapt based on target locations. For example, area cursors are the idea of having a mouse cursor represent an entire two-dimensional space rather than a single point, reducing the distance to targets. These have been applied to help users with motor impairments ^{7 7}

Leah Findlater, Alex Jansen, Kristen Shinohara, Morgan Dixon, Peter Kamb, Joshua Rakita, Jacob O. Wobbrock (2010). Enhanced area cursors: reducing fine pointing demands for people with motor impairments. ACM Symposium on User Interface Software and Technology (UIST).

Snapping is another target-aware technique commonly found in graphic design tools, in which a mouse cursor is constrained to a location based on nearby targets, reducing target distance. Researchers have made snapping work across multiple dimensions simultaneously ^{6 6}

Marianela Ciolfi Felice, Nolwenn Maudet, Wendy E. Mackay, Michel Beaudouin-Lafon (2016). Beyond Snapping: Persistent, Tweakable Alignment and Distribution with StickyLines. ACM Symposium on User Interface Software and Technology (UIST).

While target-aware techniques can be even more efficient than target-agnostic ones, making an operating system aware of targets can be hard, because user interfaces can be architected to process pointing input in such a variety of ways. Some research has focused on overcoming this challenge. For example, one approach reverse-engineered the widgets on a screen by analyzing the rendered pixels to identify targets, then applied targeted-aware pointing techniques like the bubble cursor ^{5 5}

Morgan Dixon, James Fogarty, Jacob Wobbrock (2012). A general-purpose target-aware pointing enhancement using pixel-level analysis of graphical interfaces. ACM SIGCHI Conference on Human Factors in Computing Systems (CHI).

You might be wondering: all this work for faster pointing? Fitts’ law and its focus on speed  is  a very narrow way to think about the experience of pointing to computers. And yet, it is such a fundamental and frequent part of how we interact with computers; making pointing fast and smooth is key to allowing a person to focus on their task and not on the low-level act of pointing. This is particularly true of people with motor impairments, which interfere with their ability to precisely point: every incremental improvement in one’s ability to precisely point to a target might amount to hundreds or thousands of easier interactions a day, especially for people who depend on computers to communicate and connect with the world.