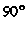 .
In this case, the cell could be specified by the parameters a,b,c,
.
In this case, the cell could be specified by the parameters a,b,c, 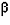 , with
, with  .
.
Symmetry and Lattices
Let's add a two-fold rotation axis to a three-dimensional lattice. Here's a general unit cell. Add a two-fold axis sticking out of the ac set of lattice lines. For the two-fold axis to generate symmetrically related lattice points, the two-fold must be perpendicular to that set of lattice lines. So the two-fold must be perpendicular to the ac plane.
Consider what that will do to the lattice points in higher levels along the b direction.
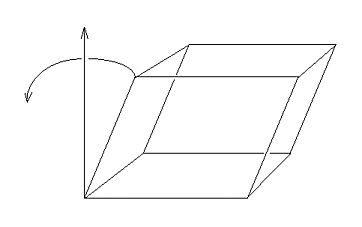
For those points to be related by the symmetry, the higher levels must have one of their lattice points right on the two-fold.
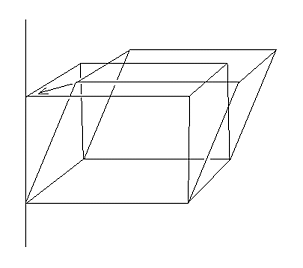
So, you could pick one of the unit cell edges such that two of the unit cell angles are
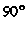 .
In this case, the cell could be specified by the parameters a,b,c,
.
In this case, the cell could be specified by the parameters a,b,c, 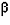 , with
, with  .
.
Here's another way to draw this and think about it.
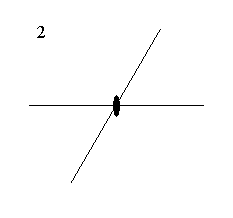
- point group 2
- forces two of the angles to be 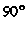
- monoclinic is the word to describe this type of lattice
- 
So what happens when you have two perpendicular two-fold axes?

- point group (222) includes a third two-fold
- three angles are 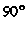
- orthorhombic lattice
- 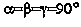
What happens when you have four-fold rotational symmetry in a lattice?

- point group 4
- forces all the angles to be 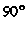
- also requires that a=b
- tetragonal lattice
What about a mirror?

- point group m (if perpendicular to another element like 2, the symbol becomes 2/m) - requires that the axis out of the plane be perpendicular to it
So what does this all mean?
If objects pack together utilizing particular symmetry operations, these will force certain
conditions to hold for the lattice and introduce conditions among the unit cell dimensions.
So from the symmetry, you can deduce things about the lattice. Note: it's dangerous to
determine the unit cell dimensions and then deduce something about the symmetry. For
instance, two of the cell angles might be 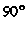 , but that doesn't mean the cell is necessarily
monoclinic. You need other information about the symmetry from the diffraction pattern
to confirm the symmetry.
, but that doesn't mean the cell is necessarily
monoclinic. You need other information about the symmetry from the diffraction pattern
to confirm the symmetry.
 back to index
back to index
 next topic
next topic
 previous topic
previous topic
copyright © Ron Stenkamp stenkamp@u.washington.edu Most recent update 1/4/99