Back to the Electron Density Equation
OK, back to the equation.
We understand the left hand side of the electron density equation, right? The electron density is a three-dimensional function in "real space". The coordinates in this equation are fractional coordinates along the unit cell edges and need not be orthogonal.
Now, the right hand side of the equation.
Over here we're going to do some sums over h,k, and l, the indices or coordinates in what's called "reciprocal space". This is the space containing the diffraction pattern. We'll see later why it's called "reciprocal space", but the thing to note is that distances in this space are inversely related to distances in "real space".
The first item on the right though is a "real space" quantity, V, the volume of the unit cell. So that gives us the 1/V in the electron "density". It must be the rest of this expression that gives us the "electrons" in "e/Å3".
So what about the other things on the right?
is something called the "structure factor". It's a description of
the scattered X-rays and has two components, a structure factor amplitude, 
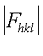, and a
phase,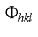 
. The amplitudes are proportional to the square root of
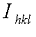, the intensities
of the spots in the diffraction pattern. These are determined from intensity measurements
of each spot in
the diffraction pattern.
So, h,k,l are indices assigned to each spot and are coordinates in reciprocal space. For what we're most concerned with, these are integers spanning the diffraction pattern. Each spot (or "reflection" (more about that later)) has unique indices assigned to it.
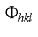is the phase of each reflection. This is the information that's
lost in the
diffraction experiment and needs to be regenerated somehow for the electron density
calculation. We'll
have a lot more to say about this "phase problem" later in the course. There are a number
of ways
available for solving the "phase problem" that we'll cover then. For now, just assume
we've somehow
obtained phases for this calculation.
is the term involved in the Fourier series. It involves the
product of the
coordinates in both "real" and "reciprocal" space. For those of you used to Fourier series,
you can think of
this expression as simply a Fourier series with structure factors ()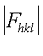
as the
coefficients.
back to index
next topic
previous topic
copyright © Ron Stenkamp stenkamp@u.washington.edu Most recent update 4/1/03