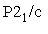
Building

Another Space Group Exercise:

Let's see if we can generate the pictures and equivalent positions for this space group just starting with the space group symbol, .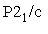

Let's start with a monoclinic unit cell, looking down the b axis with an object at x,y,z.

Let's put a two-fold screw axis along b at the origin of the cell. Operation of the two-fold screw on the first position generates one at -x,1/2+y,-z.

If you consider the contents of the neighboring unit cells, you see there are several two-fold screw axes parallel to b.

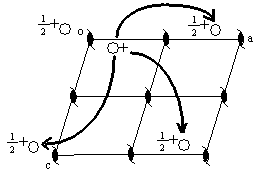
Now, add the c-glide. It's a glide plane perpendicular to b, with the glide translation along the c-axis. The glide operation on the two equivalent positions in the cell generate two more. It takes the object at x,y,z to one at x,-y,z+1/2. Likewise, an object at -x,1/2+y,-z is related to one at -x, 1/2-y,1/2-z.

So, there are four equivalent positions. Knowing a bit of what to look for, you can see that there are centers of symmetry in this unit cell. One of them is at 0,1/4,1/4 and the others are related to it by translations of 1/2 along the cell edges.

So the unit cell picture looks like this:

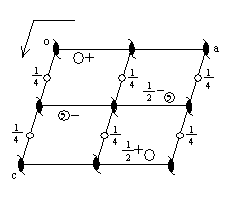
As I stated before, there's a convention that centers of symmetry should be placed at the origin. After translation to put the center of symmetry at the origin, the cell looks like this:

Now we should transform the coordinates we've generated and see if they match up with those given in the International Tables.

Our current set of coordinates is:

Now subtract 0,1/4,1/4 from each of them.

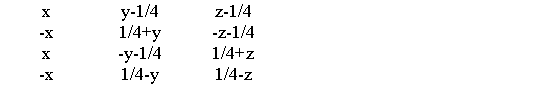
These don't look like those listed in the Tables, but if we substitute X for x, Y for -y-1/4 and Z for z+1/4, the coordinates change to:

And these match the ones in the Tables (x,y,z; -x,y+1/2,-z+1/2; -x,-y,-z; x,-y+1/2,z+1/2). (Remember: things like z-1/2 are equivalent to z+1/2 due to the unit cell translations.)

back to index

next topic

previous topic

copyright © Ron Stenkamp stenkamp@u.washington.edu Most recent update 1/17/97