Plato’s Cosmology: The Timaeus

The Forms vs. the Cosmos

The world of Forms

  1. The world of being; everything in this world “always is,” “has no becoming,” and “does not change”(28a).
  2. It is apprehended by the understanding, not by the senses.

The physical world (= the Cosmos)

  1. The world of becoming; everything in this world “comes to be and passes away, but never really is” (28a).
  2. It is grasped by opinion and sense-perception.
  3. The cosmos itself came into being, created using as its model the world of Forms.

The Demiurge (Creator)

Literally, “craftsman.” The creator of Plato’s physical world is not a divine intelligence or a personal ruler, but (as it were) a manual laborer. Cf. Vlastos, Plato’s Universe (pp. 26-27):

That the supreme god of Plato’s cosmos should wear the mask of a manual worker is a triumph of the philosophical imagination over ingrained social prejudice. ... But this divine mechanic is not a drudge. He is an artist or, more precisely, what an artist would have to be in Plato’s conception of art: not the inventor of new form, but the imposer of pre-existing form on as yet formless material.

The Elements

Features of the Cosmos

A living being

Because it is based on the Form of living being (= Animal)

Unique

Because it is based on a unique model (the Form of living being), and the Demiurge makes it as much like its model as he can (subject, of course, to the limitations imposed by the fact that it’s made of matter).

It has a soul

Because it is a living being

Spherical

Because that is the most perfect and most beautiful shape

Temporal

That is, there is time in the cosmos - it is characterized by temporal predicates. This is because it is modeled on a Form, an eternal being.

The cosmos cannot be eternal, as a Form is, since it comes into being. But it is as much like a Form, as close to being eternal, as it can be (37d). When the Demiurge created the universe, he also created time. But what is Plato’s definition of time?

Plato's text at 37d reads:

[the Demiurge] began to think of making a moving image of eternity: at the same time as he brought order to the universe, he would make an eternal image, moving according to number, of eternity remaining in unity. This, of course, is what we call “time.”
But what is ‘this’? It is sometimes thought that it refers to ‘number’, which would make the definition be that time is the number according to which the image of eternity moves. This would bring Plato's definition close to Aristotle’s (“time is the number of motion (change) in respect of before and after” [Physics 219b2]). On this reading, it is the cosmos that is the “moving image of eternity,” and time is the number that measures the change in the cosmos.

But ‘this’ has been traditionally taken to refer to ‘image’, and on this reading, Plato’s definition is that time is a moving image of eternity. Even if Plato’s text is grammatically ambiguous, the most plausible way to understand the definition is the traditional one. Other passages in the Timaeus make it clear that Plato thought of time as a kind of celestial clockwork - that is, a certain kind of motion, rather than a measure of motion.  Consider 38d and 39d:

[The Demiurge] brought into being the Sun, the Moon, and five other stars, for the begetting of time. These are called “wanderers” [planêta], and they stand guard over the numbers of time. … And so people are all but ignorant of the fact that time really is the wanderings of these bodies.

Plato clearly says that time is the wanderings of these bodies - their movement - and not a kind of number that measures such movement. Abstracting time from motion was an innovation of Aristotle’s. For Plato, time just is celestial motion.

Note that time applies, strictly speaking, only to the realm of becoming.  About the Forms, which are everlasting, we say “is, and was, and will be,” but, strictly speaking, only “is” is appropriate (38a). That is, the ‘is’ we use about the Forms is a tenseless ‘is’; the Forms themselves are, strictly speaking, outside of time.

The Heavenly Bodies

Plato’s account includes the origin of the stars and planets - “to set limits to and stand guard over the numbers of time” (38c) - which we will skip over here.

Human Beings: Souls, Bodies, and their Parts

Four kinds of living creature (39e-40b)

  1. Heavenly gods
  2. Winged things
  3. Water creatures
  4. Land creatures

Human soul (40d-44d)

  1. Creation and destruction of the gods (40d-41a)
  2. Demiurge instructs gods to make mortals (41a-d)
  3. Human souls manufactured
    • Made of leftovers from manufacture of world-soul, but of a lower grade of purity (41d).
    • Each soul assigned to a star (41e).
    • Death: a just soul returns to its companion star, an unjust soul is reincarnated for a second try (42b-c).

Human body (44d-47e)

  1. Head and limbs (44d-45b)
  2. Eyes and vision (45b-46a)
  3. Purposes of seeing and hearing (46c-47e)

The Structure of Matter

At this point Plato ends his discussion of the “works of intellect (nous)” and begins discussing the “works of necessity”. The difference seems to be that the former, but not the latter, directs its creation with an eye toward what is best.

Here Plato turns to the old Presocratic question: what is the world made of? His answer both combines and transcends theirs. It mentions the traditional Earth, Air, Fire, and Water (of Empedocles), but goes beyond them, analyzing them in terms of mathematical objects (shades of the Pythagoreans) and empty space (the invention of the atomists).

The four elements

The intrinsic nature of fire, water, air, and earth (48b), and how they came into being.

The receptacle

A new concept is introduced, in addition to the model (= the Forms) and the imitation of the model (= the world of becoming): “the receptacle of all becoming” (49a).

The receptacle is that in which all becoming takes place. The fires that you see coming into being and being extinguished are just appearances, in the receptacle, of the Fire Itself (the Form).

At 52b ff, Plato describes the receptacle as “space.”

The coming to be of the elements

The four elements are “the most excellent four bodies that can come into being” (53e). But how do they come into being? What are they made of? Plato’s answer is that they are all made of triangles, and constructed in such a way as to explain how the transmutation of elements is possible.

Overview

Each kind of matter (earth, air, fire, water) is made up of particles (“primary bodies”). Each particle is a regular geometrical solid. There are four kinds of particles, one for each of the four kinds of matter. Each particle is composed of elementary right triangles. The particles are like the molecules of the theory; the triangles are its atoms.

The argument that all bodies are ultimately composed of elementary right triangles is given at 53c-d: all bodies are 3-dimensional (“have depth”) and hence are bounded by surfaces. Every surface bounded by straight lines is divisible into triangles. Every triangle is divisible into right triangles. Every right triangle is either isosceles (with two 45° angles) or scalene. So all bodies can be constructed out of isosceles and scalene right triangles.

The details

  1. The two atomic triangles
    Plato notes (54a1) that there is only one kind of isosceles right triangle--namely, the 45°/45°/90° triangle--whereas there are “infinitely many” kinds of scalene. But of these, he tells us, “we posit one as the most excellent” (54a7), one “whose longer side squared is always triple its shorter side” (54b5-6). Plato describes the same scalene triangle, equivalently, as “one whose hypotenuse is twice the length of its shorter side” (54d6-7). (The angles of this triangle are thus 30°/60°/90°.)

    I’ll call the 30°/60°/90° triangles “a triangles” and the 45°/45°/90° triangles “b triangles.”
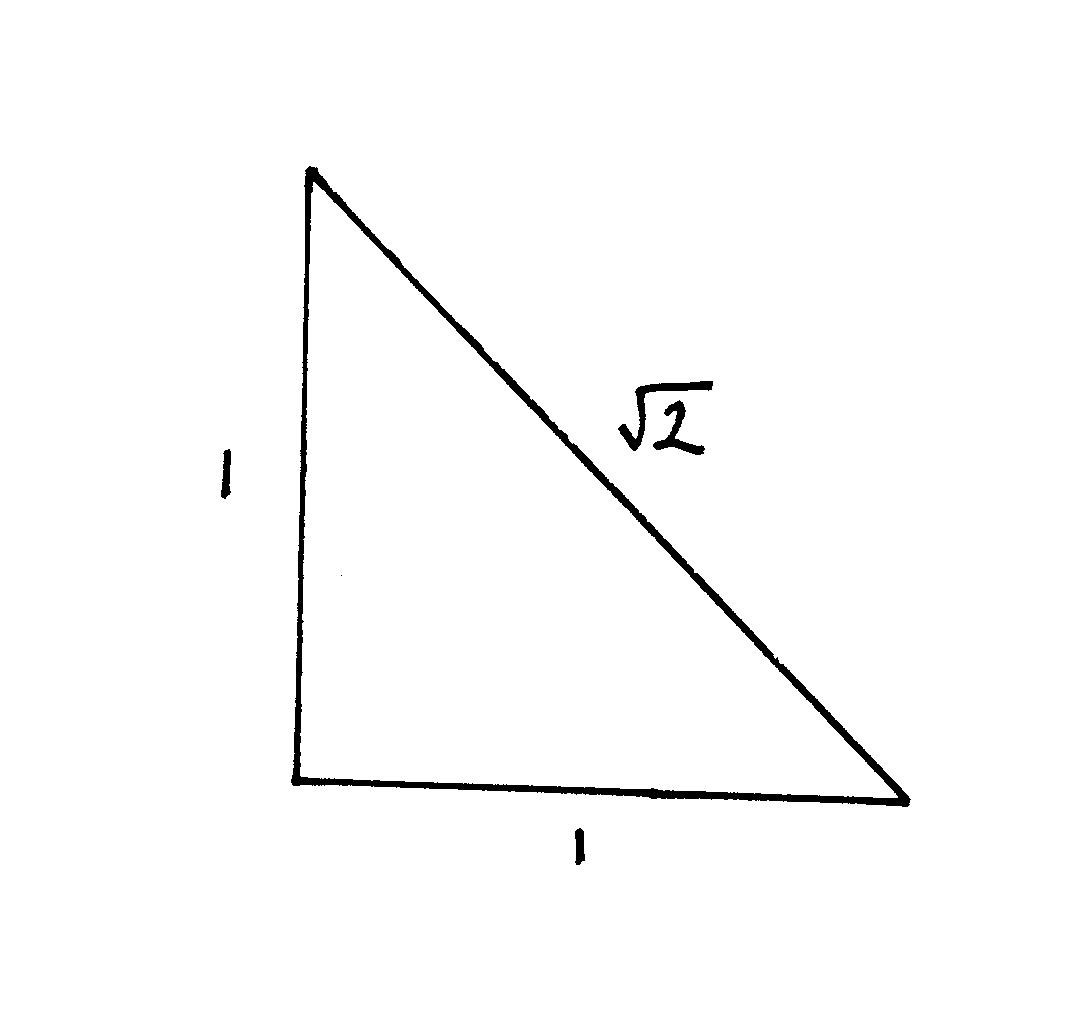    Scalene (a) triangle Isosceles (b) triangle
    a triangle (scalene, 30°/60°/90°) b triangle (isosceles, 45°/45°/90°)

  2. Construction of “faces” of particles out of the atomic triangles
    • Each face is either an equilateral triangle (t) or a square (s).

    • Equilateral triangles (t’s) are made of a triangles.

    • Squares (s’s) are made out of b triangles.

    • Plato’s description at 54e and 55b tells us that each t is made of 6 a’s, and each s is made of 4 b’s. (See diagrams, RAGP 640.) But 57c-d makes clear that he envisages other ways of constructing these faces out of primitive a’s and b’s.

  3. Construction of solid particles out of the faces
    The construction of the particles is described at 54d-55c. The particles are identified with the four elements at 55d-56b. Click on the names of the elements to see a diagram of a particle of that element:

    1. Fire: a particle of fire is a tetrahedron (4-sided solid), made of 4 t’s consisting of 24 a’s altogether.

    2. Air: a particle of air is an octahedron (8-sided solid), made of 8 t’s consisting of 48 a’s altogether.

    3. Water: a particle of water is an icosahedron (20-sided solid), made of 20 t’s consisting of 120 a’s altogether.

    4. Earth: a particle of earth is a cube (6-sided solid), made of 6 s’s consisting of 24 b’s altogether.

  4. Transformation of elements (described at 56c-57c)
    Inter-elemental transformations are among fire, air, and water only. Earth cannot be transformed into any of the others (54c, 56d).

    Transformations can be described at the level of equilateral triangles (that are the faces of the three solids). Since a fire molecule has 4 faces (one F is made up of 4 t), an air molecule 8 (one A is made up of 8 t), and a water molecule 20 (one W is made up of 20 t), any of the following transformations (for example) are possible.  (Each transformation is represented by an equation on the left; its geometrical basis is shown by the equation on the right.):

    1 A = 2 F

    8 t = 2 × 4 t

    1 W  = 5 F  

    20 t = 5 × 4 t

    2 W  = 5 A

    2 × 20 t = 5 × 8 t

    1 W  = 2 A + 1 F

    20 t = (2 × 8 t) + 4 t

    1 W  = 3 F + 1 A

    20 t = (3 × 4 t) + 8 t

  5. Larger and smaller particles
    Since equilateral triangles can be constructed out of a’s (and squares out of b’s) in more than one way, it is possible to have “molecules” of each of the elements that have different numbers of atomic triangles (a’s and b’s). These might be considered “isotopes” of the basic molecules described by Plato (with each t made of 6 a’s, and each s made of 4 b’s).

    An equilateral triangle can also be constructed out of 2, or 8, or 18, a’s (and so on, ad infinitum).

    A square can also be constructed out of 2, or 8, or 16, b’s (and so on, ad infinitum).

    This means that one “normal” particle of earth (6 s = 24 b) can be transformed into 2 of the smaller “isotopes” of earth (6 s = 12 b)

    Similarly, 4 “normal” particles of water (containing 120 a’s each) can combine to form one huge particle of one of the larger “isotopes” of water (20 sides of 24 a’s each, for 480 a’s altogether).

Final Reflections

Comparison with predecessors

Plato’s theory combines elements of the views of many of his predecessors.

  1. Pythagoras
    Like Pythagoras, he made the physical universe fundamentally mathematical. But whereas Pythagoras thought that everything was made of numbers, Plato made geometrical figures - ultimately, triangles - the atoms of his system.

  2. Democritus
    Plato, like Democritus, was an atomist. But whereas Democritean atoms were of all different shapes and sizes, Plato’s came in just two varieties: isosceles and scalene. In this respect, Plato’s theory was far more elegant than that of Democritus. As Vlastos comments (Plato’s Universe, pp. 93-4):
    Compare [Plato’s theory] with the best of its rivals, the Democritean. There atoms come in infinitely many sizes and in every conceivable shape, the vast majority of them being irregular, a motley multitude, totally destitute of periodicity in their design, incapable of fitting any simple combinatorial formula. If we were satisfied that the choice between the unordered polymorphic infinity of Democritean atoms and the elegantly patterned order of Plato’s polyhedra was incapable of empirical adjudication and could only be settled by asking how a divine, geometrically minded artificer would have made the choice, would we have hesitated about the answer?
  3. Empedocles
    Like Empedocles, Plato recognized that four elements - earth, air, fire, and water - underlay all physical changes. But unlike Empedocles, he found a common atomic ingredient underlying the elements. Hence, unlike Empedocles, he could explain the transformation of one element into another.

Problems and Responses

Plato’s theory of matter faces some prima facie problems.  We will consider two of them and suggest how Plato might have responded to them.

  1. Problem: Plato’s theory does not allow for transformation of earth into other elements.

    Since earth is made of different atoms (isosceles triangles) from the other elements (scalene triangles), this transformation is impossible, as Plato knew. So what happens when, e.g., wood burns? Isn’t earth (which is what, presumably, wood is mostly made of) converted into fire?

    Response: The transformation of one element into another is not an observed phenomenon, but a theoretical explanation of observations. Plato can account for this phenomenon by theorizing that it is the water and air components of wood that are converted into fire; the earth components remain unburned in the ashes that remain.

  2. Problem: The transformation of elements seems to violate the principle of conservation of matter.

    The problem here is that the volumes of the polyhedra in Plato’s “equations” don’t add up correctly. E.g., consider the “equation”:

    1 W = 3 F + 1 A

    which tells us that one water atom can be converted into 3 fire atoms and one air atom. (There are 20 equilateral triangles, t, involved in this equation.) The problem is that the volume of one water atom (i.e., one icosahedron) is much greater than the combined volumes of 3 fire atoms (3 tetrahedra) and one air atom (one octohedron). If we let s be the length of a side of each equilateral triangle (t) that is a face of each of the polyhedra, we can calculate these volumes:

    Volume of 1 W = 2.1817 s3

    Aggregate volume of 3 F + 1 A = .8248 s3

    Response: Remember that matter is not a concept Plato is working with. Hence matter, as we understand it, is not what Plato needs to worry about conserving.  In his view, a material object consists, ultimately, of the triangular atoms composing the polyhedral corpuscles of the four different elements. Contained within these polyhedra is empty space - the receptacle, as he called it.

    So it is not matter that Plato must conserve, but triangles. On his theory, when a corpuscle of water is broken down and converted into corpuscles of fire and air, all of the original triangles in the corpuscle of water are conserved. And the triangles combine to form the surfaces of the polyhedra. Hence it is not the total volume of his polyhedra, but their combined surface area that must be conserved. What remains constant in every transformation, as Vlastos (Plato’s Universe, p. 90) says, is:

    ... the aggregate surface area of the corpuscles. If you press him to say what happens to that portion of the matter within the icosahedron which cannot be enclosed within the equivalent surface area of smaller polyhedra, Plato would say that there is no such matter: after creation matter exists only in the form of space encapsulated by polyhedra; what is not thus encapsulated is empty space, which becomes matter when captured by envelopes of the approved stereometric form.

Go to next lecture on Aristotle’s Categories

Go to previous lecture on the Third Man Argument

  Return to the PHIL 320 Home Page

Copyright © 2006, S. Marc Cohen