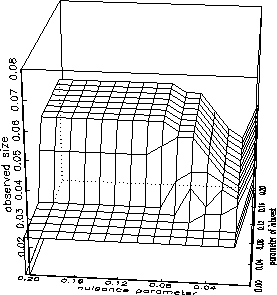
Figure 4: Size of confidence region of constrained parameter of interest in the presence of a constrained nuisance parameter
One should expect the behavior of the likelihood ratio statistic to be quite complex when both parameters are in the region of their boundaries, and this is confirmed in a Monte Carlo analysis.
The true values of the two means of a bivariate unit Normal distribution with correlation .9 were varied from 0 to .18 in 9 intervals. 500 samples of size 300 were drawn for each of these 225 sets of means. The 95 percent confidence intervals were computed by inversion of the likelihood ratio statistic, and the observed proportion of the intervals that failed to contain the true value are plotted in Figure 4.

Figure 4: Size of confidence region of constrained parameter of interest in
the presence of a constrained nuisance parameter
Departures from nominal size are indicated by deviations from a flat plane set to .05. It is easily observed that relationship to nominal size is quite complex. There is no known method to compensate for this deviation. As with Case 2, however, departures from nominal size are trivial when the correlations between the parameter of interest and the nuisance parameter are less than about .7.