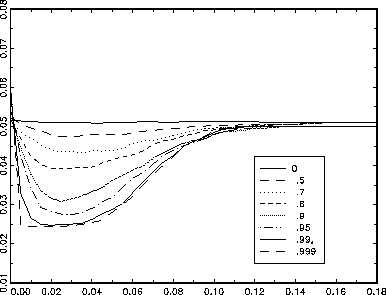
Figure 3: Size of confidence region of unconstrained parameter in the presence of a constrained nuisance parameter
When a constrained nuisance parameter is in the region of a constraint boundary, the confidence limits of a model parameter are affected even when the parameter is itself unconstrained. This fact is established when the true value of the nuisance parameter is on the boundary (Gourieroux, et al. (1982), Self and Liang (1987), and Wolak (1991)). When the parameter of interest and the nuisance parameter are uncorrelated, however, the effect vanishes.
A Monte Carlo study was conducted to determine possible effects of a constrained nuisance parameter in the region of a constraint boundary on the size of the confidence limits of an unconstrained parameter of interest. The true value of the constrained nuisance parameter varied from 0 to .18 in 37 intervals, and the correlation between the nuisance parameter and the constrained parameter of interest varied in 8 intervals from 0 to .999. 10,000 samples of size 500 were drawn under each of the conditions for a total of 2,960,000 samples. The results are presented in Figure 3.

Figure 3: Size of confidence region of unconstrained parameter in
the presence of a constrained nuisance parameter
The abscissa represents the true value of the constrained nuisance parameter, and the ordinate represents the observed size of the distribution of confidence intervals for the parameter of interest, that is, the proportion of intervals that fail to contain zero, the true value of the parameter of interest. The different curves show this relation at different correlations between the nuisance parameter and the parameter of interest.
We see from Figure 3 that any correction for size
for a true value of the nuisance parameter on the boundary
is not generalizable to true values in the region of the boundary,
as it was for Case 1. In fact, effects on size in the region
of the boundary are nonlinear and much larger than the effects
on the boundary.
This means that the corrections to the inversion of
the chi-square statistics discussed in Gourieroux, et al. (1982)
and Wolak (1991) are not applicable to
cases where the true value of the correlated nuisance parameter
falls within ![]() of the constraint boundary.
of the constraint boundary.