The GARCH model for time series contains several highly constrained parameters. This example presents estimates and confidence limits for a GARCH(1,1) model applied to 20 years of monthly observations on the capitilization weighted returns of the Wilshire 5000 index.
Define the time series
![]()
where t = 1, 2, ... T, and ![]() an observed time series with expected value
an observed time series with expected value ![]() .
.
Further define
![]()
where ![]() ,
, ![]() , and
, and
![]()
The log-likelihood conditional on max(p,q) initial estimates of the
conditional variances is, for ![]()
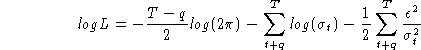
The customary constraints applied to the parameters to enforce stationarity and a positive conditional variance are

To be able to construct a uniform prior, it is necessary
to bound ![]() from above and
from above and ![]() from above and below.
For the example,
from above and below.
For the example,

were added.
The prior, then, is constructed from the above constraints:
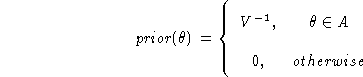
where A is the hypervolume inscribed by the inequalities, and V = 400 for this example.
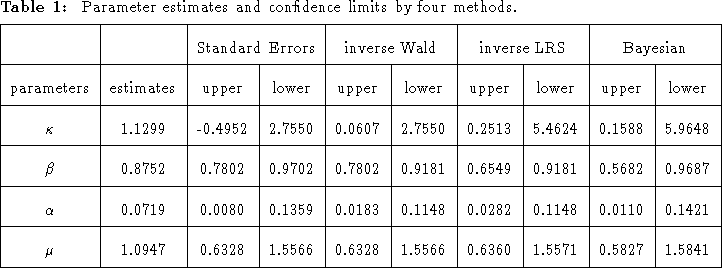
The parameter estimates are presented in Table 1 along with confidence
limits computed by four different methods. It can be observed there that
the confidence limits of the structural parameter, ![]() , is very consistent
across the methods.
, is very consistent
across the methods. ![]() is not itself constrained. However, it's confidence
limits can be affected by estimates of the remaining parameters occuring in the region
of their constraint boundaries. This, however, is provided that the distribution
of
is not itself constrained. However, it's confidence
limits can be affected by estimates of the remaining parameters occuring in the region
of their constraint boundaries. This, however, is provided that the distribution
of ![]() is correlated more than about .7 with these parameters. Table 2 presents the estimate
of the correlation matrix of the parameters calculated from the maximum likelihood estimate. We see
there that the largest correlation is quite small, -.05, and thus we should expect
that the constraints on the remaining parameters will have little effect on the
structural parameter.
is correlated more than about .7 with these parameters. Table 2 presents the estimate
of the correlation matrix of the parameters calculated from the maximum likelihood estimate. We see
there that the largest correlation is quite small, -.05, and thus we should expect
that the constraints on the remaining parameters will have little effect on the
structural parameter.

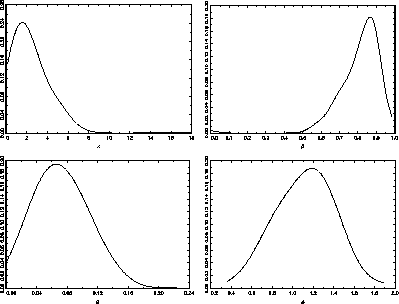
Figure 6: Kernel density plots of the parameters of a GARCH(1,1) model of
the Wilshire 5000 capitalization weighted returns
Kernel density plots were constructed for each of the parameters from
the weighted likelihood bootstrap results (Figure 6). The posterior distribution
of ![]() appears to be slightly skewed resulting in a slight difference
between the mean and the mode. The mean of the distribution, 1.1167, is very
close to the maximum likelihood estimate, 1.0947. The mode, however, appears
to be about 1.2.
appears to be slightly skewed resulting in a slight difference
between the mean and the mode. The mean of the distribution, 1.1167, is very
close to the maximum likelihood estimate, 1.0947. The mode, however, appears
to be about 1.2.