`mmf.math.integrate.integrate_1d.clenshaw_curtis`¶

`sp`
`np`
`clenshaw_curtis`(f, n)	Return the integral of 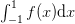$\int_{-1}^{1}f(x)\d{x}$ .

Clenshaw-Curtis integration.¶

This is a quadrature method for evaluating integrals over [-1,1] using the change of variables 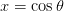$x=\cos\theta$ :

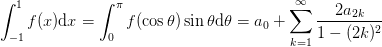
$\int_{-1}^1 f(x) \d{x} = \int_0^{\pi} f(\cos\theta)\sin \theta\d{\theta} = a_0 + \sum_{k=1}^{\infty}\frac{2a_{2k}}{1-(2k)^2}$

where the coefficients 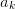$a_k$ are the cosine series

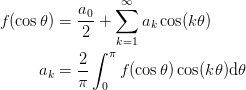
$f(\cos\theta) &= \frac{a_{0}}{2} + \sum_{k=1}^{\infty} a_k\cos(k\theta)\\ a_k &= \frac{2}{\pi}\int_0^\pi f(\cos\theta)\cos(k\theta)\d{\theta}$

which can be computed using the Fast Fourier Transform (fft).

mmf.math.integrate.integrate_1d.clenshaw_curtis.clenshaw_curtis(f, n)[source]¶

Return the integral of $\int_{-1}^{1}f(x)\d{x}$ .

Parameters :

f : function

n : int

Number of quadrature points is n+1.