Finding the Distance
Parallax
Parallax is one of the easier distance finding methods in astronomy. It is useful for finding the distance to stars that are fairly close, and is surprisingly accurate.
Parallax is based on the fact that nearby objects will appear to move faster than far away objects. We have all experienced this effect on our own driving in our cars; street signs and trees near the side of the road speed past us while the mountains and buildings in the distance hardly move. We can apply the same effect to the stars to find their distances. As Earth orbits the Sun, the stars that are closest to us will appear to move the most across the sky, while the far away stars will hardly move. The image below illustrates this nicely:
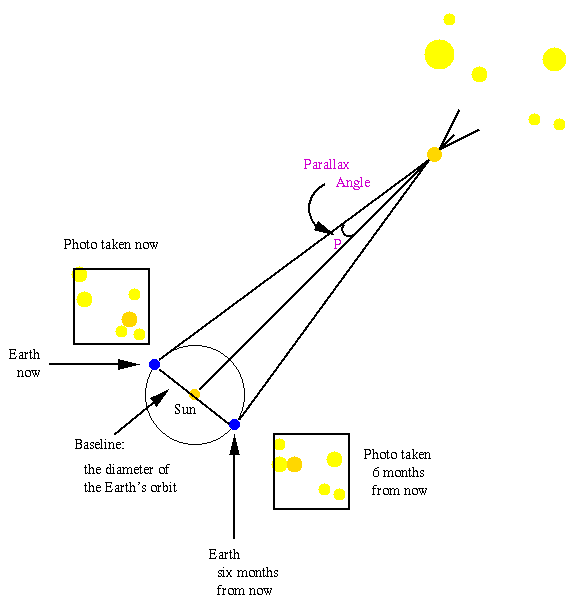
Figure 1: Image courtesy of University of Maryland
If we take an image of a nearby star in June and take another image six months later in December, we will see our star appear to move across the sky as shown in Figure 1. We use "background" stars as a reference, since we assume they are so far away they will not move at all as we orbit the Sun. These stars are fixed in place, and if we can measure the difference in position of our nearby star with respect to the fixed background stars, we can find its distance. We use the following equation to find distance:
d = 1/pd gives the distance in parsecs, and p is the parallax angle in arcseconds. As you can see, this is a simple and neat formula, and the only needed observational variable is the parallax angle. From Figure 1 you can also see how the parallax angle increases with the baseline, so we use the biggest one we can: the Earth's orbit.
Using Parallax
The closest star to Earth, other than the Sun, is Proxima Centauri. It is part of a triple star system, with Alpha and Beta Centauri, and has a parallax angle of about 772.3 milliarcseconds, or 0.7723 arcseconds. The distance to Proxima Centauri, is then
d = 1/0.7723d = 1.294 parsecs