Question 1: For stars with 0.2 < g - r < 0.4, plot ln(Rho) vs. Z , where Rho is the stellar number density in a given bin (e.g. look at Figs. 5 and 15 in JuriŽ et al. 2008, ApJ, 673, 864 for similar examples). You can approximate Rho(Z) = N(Z)/V(Z ), where N(Z) is the number of stars in a given bin, and V(Z) is the bin volume (note that the solid angle is ~ 314 deg ). What is the Z range where you believe the results, and why?

References:
http://www.astro.washington.edu/users/ivezic/SDSSReferences/tomographyII.pdf
http://www.astro.washington.edu/users/ivezic/SDSSReferences/tomographyI.pdf

First we need to look through the references and find the equations mentioned in the question. These can be found at the end of the papers in the appendices.

Metallicity Equation:
[Fe/H]= -13.13 + 14.09*x + 28.04*y - 5.51*x*y - 5.9*x^2 58.68*y^2 +9.14*x^2*y -20.61*x*y^2 +58.2*y^3
x= u filter- g filter
y= g filter- r filter
if g-r < 0.6, ignore this equation and use Fe/H=-0.6

Absolute Magnitude Parallax Relation From:
Ivezic et al. 2008 (ApJ, 684, 287)
delM([Fe/H])= 4.50 - 1.11[Fe/H] - 0.18[Fe/H]^2
Mr0(g-i)=-5.06 + 14.32*x 12.97*x^2 + 6.127*x^3 1.267*x^4 + 0.0967*x^5
x=g-i
Mr(g-i,[Fe/H])=Mr0(g-i)+delM([Fe/H])

First we import the .dat file into our array manipulator, and make three new columns- one for each color u-g,g-r,and g-i. Find the absolute magnitude Mr for all the stars using the 4 equations above, and then use the distance modulus to find D: r - Mr = 5 * log (D/(10pc)) Once you do this, restrict the data between 0.2 < g-r < 0.4. Then create bins based on the Z value for these targets spanning a range of 500 parsecs for each bin in Z. You can use loops to do this, but another way is to make a histogram and simply output the number of stars in each bin. Rho=# of stars in the bin/bin volume, using radians. Plot the ln(Rho) vs. Z. Your plot should look something like this:

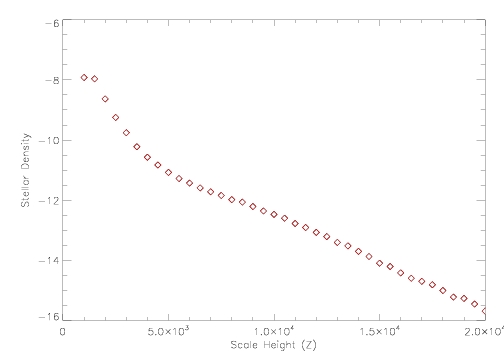
It is fairly hard to tell, but we would expect that the density would drop off quite rapidly when leaving the disk. We see this happen until we hit about 5 kiloparsecs, when the decrease in density starts to level off at a more gradual rate. Question two will give us a more exact answer of what is happening.

---

Back Next