This paper appears as chapter 16 in D. Levine, V. R. Brown and V. T. Shirey (eds), Oscillations in Neural Networks, Lawerence Erlbaum and Associates, Publishers

©, 1999. Lawerence Erlbaum & Associates, Mahwah, NJ. 1999.

Foraging Search at the Edge of Chaos

George E. Mobus
Western Washington University

Paul S. Fisher
University of North Texas

Many animal species are faced with the problem of finding sparsely distributed resources that occur (and disappear) dynamically in a huge space. Furthermore the dynamics of these resources are stochastic and probably chaotic in terms of both spatial and temporal distribution. But they are not completely random. The search strategy is called foraging. It involves two interrelated phases which dominate the behavior of the animal based on the amount of knowledge it has regarding the location and timing of the resource. In the absence of knowledge or cues foraging animals adopt a stochastic search pattern that will have a reasonably high likelihood of bringing them into encounters with the resource. With knowledge or cues, the animal switches to a more directed search behavior.

Autonomous agents such as mobile robots may need to have these capabilities in order to find mission-critical objects yet no current algorithmic or heuristic search method adequately addresses this problem. The serendipitous discovery of a quasi-chaotic oscillating neural circuit used to generate motor signals in a mobile robot has led to the development of an autonomous agent search method that resembles foraging search in a number of details.

An oscillator circuit, based on the concept of a central pattern generator (CPG) in biology, is described qualitatively. Its role in controlling the motion of a mobile robot and the effects it has on search efficiency are presented. Constraining search to potentially fruitful paths before any useful heuristics are available to the searcher is a problem of general interest in artificial intelligence. Foraging search based on chaotic oscillators may prove useful in a more general way.

1. INTRODUCTION

Quite typically, mobile robots that search for objects in their environment are programmed to scan the vicinity and, if they spot what they are seeking, plan a movement path to the object. If they do not sense their target object, they plan a movement path that will position them at a new observation point. Most often, these programs seek an optimal path between the two points. These approaches are computationally expensive. In stark contrast, many animals, when searching for food or other resources, exhibit seemingly non-optimal movements. They can be seen to weave and wander, sometimes erratically, through their search space. Animals are, however, generally successful in finding the resources they seek in spite of this seeming non-optimal pattern of search behavior[1]. Many animal species forage for critical survival resources such as food, water and shelter, as well as what might be called mission resources such as mates or nesting material.

Foraging is a search strategy that is employed when the subject knows what object is being sought but doesn't necessarily know where, in a usually vast space, to look. Further characteristics that make this search problem of general interest is that the resources often are sparsely distributed and may have chaotic dynamics with respect to their location, duration and timing. Foraging for resources in a chaotic [2] world may be the quintessential task for any autonomous agent, natural or artificial. We have been developing an artificial agent that is strongly inspired by biological models, an embodied (Brooks, 1991) Braitenberg (1984) vehicle, which is designed to learn how to perform a basic search mission in a non-stationary environment. The 'robot' is called MAVRIC (Mobile, Autonomous Vehicle for Research in Intelligent Control) (Mobus & Fisher, 1993; 1994). The motivation for this objective comes directly from the observation that the 'real' real world is open from the point of view of any realizable agent. Extending Brooks' (1991) notion of situatedness as a precondition for the successful demonstration of intelligence in artificial systems, we believe that ongoing real-time adaptation is an open-ended process that must extend over the life of an agent. In other words, we do not subscribe to the notion that artificial agents will be trained on some fixed set of patterns (even if only trained on some subset of the universe of patterns) and then be ready to survive in the real world. Things change too much even in environments that we know fairly well. Or in worlds we have not even adequately explored, things may be too different from our expectations to allow us to choose adequate training sets.

In foraging, animals may start with little or no knowledge of the organization of the environment. That is, they are not familiar with cue-resource relationships (situational heuristics) initially[3]. As they conduct their unguided search and then encounter the sought resource, they learn which cues (or landmarks) can be reliably counted on to lead to the sought resource and so they tend to improve their performance on subsequent searches. As they gain knowledge of these situational heuristics, they can use them to guide their searches. Should conditions change and the learned cue-resource relations no longer hold, animals revert to their uninformed search strategy and begin the process of learning the new cues. Our work centered on a neuromimic adaptive processor that allows an agent to learn the cue-resource relationships in a non-stationary environment such as this. The adaptive element of the neuromime, taking the place of a traditional synaptic weighting function, is called an Adaptrode (Mobus, 1994a; 1994b).

An adaptrode models the multiple time-scale memory trace mechanisms operative in the post-synaptic compartment of neurons (Alkon, 1987). Mathematically it is a cascaded, modified exponential smoothing function for pulse-coded primary input signals. Each level in the adaptrode corresponds to a longer time scale so that the adaptrode captures moving average activity over short-, intermediate- and long-term periods. The smoothing functions at each level are gated into the next longer time scale by the receipt of a second, temporally-ordered[4], correlated signal to achieve associative learning. The adaptrode response to primary input (specifically the cue signal) is, thus, dependent on the history of inputs with higher weight given to more recent activity and longer-term weighting dependent on correlation with other signals (specifically resource detection signals that come some short time after excitation of the cue signal). Adaptrode response to input is effectively an estimate of the salience of the current input. It takes the place of the traditional weighted input signal in conventional neural network models. Thus weights in an adaptrode-based neuron are dynamic. They forget to the extent that recent inputs are not repeated and reinforced over time. As such they enable life-long learning networks. In previous work, Mobus (1994b) has shown that a simple two-cell network of competitive, adaptrode-based neurons can learn orthogonal associations so long as they separate in time domains. This is one solution to the destructive interference problem known to plague many conventional neural networks.

In MAVRIC, we wanted the robot to learn situational heuristics in which the detection of a cue, which is causally related to a resource event, could be used as a predictor of the location and timing of the event. Resource-cue associations in natural environments abound. Color, shape of plants, existence of a watering hole; all of these are exploited by numerous animals as cues to the potential presence of food. In our lab we arranged that light sources would be associated with (physically near) various resource objects. MAVRIC's task was to learn to find these resources by first learning the association and thereafter using the occurrence of a light as a predictor of the occurrence of the resource. Adaptrode-based neurons learn these relations in real-time and on-line. All that would be needed would be a way to get MAVRIC to experience the association a sufficient number of times so that the learning could take place.

We faced an early problem in terms of how to get the process started. It turns out that the strategy of motion of the agent before it has learned any useful relationships can have a significant impact on how quickly it is exposed to instances of successfully finding a resource and, consequently, learning the associated cues. MAVRIC, in classic Braitenberg style, uses fixed, semi-directional sensors. As a result, simply having MAVRIC move along in a straight line would severely restrict its ability to sample the space and, unless a resource (and its associated cues) happened to occur directly in its path, it would never find a resource, let alone learn cues that would lead to resources.

As an obvious starting point then, we provided MAVRIC with a random walk motor program in order to introduce some "novelty" into the search path. In this approach MAVRIC would move for a randomly chosen interval and then turn in a randomly chosen direction a randomly chosen number of degrees. It is possible to show that a random walk search is guaranteed to cover the entire space, but it may take an infinite amount of time to do so. From the standpoint of increasing the number of successful finds and subsequent learning, this method would work if we didn't care how long it took MAVRIC to find resources. The adaptrode learning mechanism is very fast at encoding associations (Mobus, 1994a; 1994b), so that after five or six encounters MAVRIC became quite good at finding the resource based on following cues. However, it might take MAVRIC several days to even locate the first such encounter by chance, let alone the five needed to get it to start following cues. Under those circumstances we followed a program of "training" MAVRIC on cue-resource relationships in which we placed the objects sufficiently close to MAVRIC so that it was guaranteed at least five encounters in a short time (Mobus & Fisher, 1991a; 1991b). Thereafter, the robot would reliably follow the learned cues if they were detected.

However, this was not a "good" solution for two reasons. First, the required training was not the same as allowing MAVRIC to learn from naturally occurring experience. We were trying to achieve the same level of autonomy as animals possess in the wild. Every time conditions changed we would have to retrain the robot. This initial approach resembled conditioned learning experiments conducted in animal learning (e.g., classical or Pavlovian conditioning) (Mackintosh, 1983), but this was not what we wanted.

Second, unless the density of resources spread throughout the environment were sufficiently high, the random walk search might still cause MAVRIC to fail to find that for which it was looking for long periods. Animals seeking food in the wild are under time and energy constraints that necessitate finding some instances of food every so often. Evolution works to match the species' search procedure-sensory apparatus and the resource density (both space and time) provided by the environment (niche). Grazing animals that are virtually surrounded by their food can accommodate nearly any strategy. Bacteria that swim in a medium relatively rich in nutrients employ a tumbling mechanism not unlike the random walk until they sense the chemical gradient leading to their food (Koshland, 1980). Sheep flocks tend to graze in "straight" lines until something (like a sheepdog) redirects their movements. Grazers do not rely on cue signals to find their food. Animals that hunt (forage) for a living rely on very different mechanisms.

Foraging is a complex behavior in most species. However the search phase can be characterized in two sub-phases depending on the animal's possession of knowledge or cues that would lead it to the resource. In the absence of knowledge or cue an animal tends to "wander" along novel paths as it attempts to perform a sensory sweep of the area. This can be observed directly by watching scout ants walking over a sidewalk or driveway. The ant does not wander aimlessly as in a random walk, rather it takes a weaving pattern, generally leading in some given direction. The path is novel (stochastic) yet follows some general pattern. Or observe a hound dog trying to pick up the scent of a prey. It will tend to weave back and forth over the area with a minimum of crossing back over its own path.

Once an animal has either acquired knowledge (e.g. honeybee workers observe the dance of a worker that has found a source of nectar) or senses the nearness of the resource (e.g., odor of food), the search becomes more directed, bringing the animal sufficiently close to the resource that the final stages involve direct sensory contact. Even with cues and/or knowledge there is still some uncertainty associated with the actual location of a resource due to imprecision in sensory measurements in navigation and communication (as in the case of the bees). Animals can be seen to continue a weaving motion, though with much lower amplitude, as they "home in" on the resource. This motion may be needed to obtain triangulation or gradient information necessary for computing the location of the object. But the existence of the motion as a gradation of that used in stochastic search is an important clue to understanding the underlying motor program generating the search patterns.

Another problem with using programmatic motor control models was interfacing the program with the neural decision process. As our robot acquired the sensory detection of a cue, how should it switch from non deterministic search mode to directed mode? The neural network itself provided information for following gradients, but it wasn't clear how to best integrate the output of the neural net with the motor control program.

As we had done in looking for solutions to the learning mechanism by turning to biological models, we started looking for neurological mechanisms that might help solve this problem. A class of neural circuits, called central pattern generators (CPGs) are oscillators that are responsible for a number of rhythmic motor functions in a wide variety of animals. We were inspired by the way a relatively simple network of neurons could produce oscillatory outputs of the (intuitively) right form. The fact that these circuits are known to be modulated by other neural inputs, hence allowing the shaping of output waveform, was another attractive feature. We decided to investigate artificial CPG circuits constructed from adaptrode neurons. It turned out to be a useful approach.

2. CENTRAL PATTERN GENERATORS

Motion in animals involve opponent processes such as opposing muscleclature or muscle-hydrostatic pressure opponents as in arachnid limb movement or cardiac pumping. Such opponent forces are mediated by neural control signals that convey the appropriate phase and amplitude information such that the direction and force of the motion achieve the desired result without overstraining the motor elements themselves. These motions often involve some degree of tension between the motors but are always coordinated so as to protect the "machinery" from undue stress. Many movements in animal behavior repertoires as well as internal functions such as cardiac pumping and digestive tract movement are oscillatory in nature.

The undulatory swimming motion of a leech, the escape swimming of the mollusk Tritonia diomedea, and the heartbeat of the lobster are known to be controlled by a type of neural circuit called a central pattern generator or CPG. In fact, such circuits are known to control a wide variety of rhythmic motions such as breathing, walking and swimming (Kleinfeld & Sompolinsky, 1989). A number of heterogeneous architectures have been described which have similar kinds of behavior. In swimming control circuits where opponent muscle groups are alternately stimulated, the architectures involve two output groups, each of which generates bursts of pulses in alternating fashion (Selverston & Mazzoni, 1989). Thus the opposing muscle groups alternately contract and relax in approximately 180 degree phase shift from each other.

The general architecture of these circuits involves multiple groups or clusters of neurons, some of which excite other groups or clusters and some of which inhibit. Feedback inhibition, in which one group excites another and the later inhibits the former, is often seen. This pattern is seen when one or both clusters involve cells with tonic activity (self-excitation). Figure 1 shows a two cell CPG of this form. Far more complicated circuits with many connections are seen in many animals.

An important feature of these circuits is the temporal behavior of connections, or synaptic dynamics. Slow and fast synapse responses are known. Thus, as in Figure 1, the excitatory synapse from A to B may operate quickly to cause B to fire, whereas the feedback inhibition on A may be slow, thus allowing B to continue being excited (and hence firing) for some time before shutting A down. The output from such a circuit appears as a half-wave.

Another extremely important aspect of many CPGs is the way in which external inputs to the circuit can cause the output form to be modulated in frequency or amplitude. Some circuits are turned on and off by outside inputs (Roberts, 1989). This feature gives these circuits considerable flexibility in responding to outside influences. Animals can change their rhythm (or gait), and speed with the same basic circuit. Such features are attractive when designing a control system.

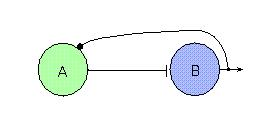
Fig. 1. A simple CPG circuit showing feedback inhibition. Cell A may be a tonically firing (self-excitatory) one which excites (flat terminal) cell B to fire. The latter then inhibits (circular terminal) cell A. Output from the circuit (pointed arrow) shows an episodic burst pattern.

3. AN ADAPTRODE-BASED CPG

Oscillatory motion would be a desirable approach to causing a fixed-sensor robot such as MAVRIC to perform a sensory "sweep" of its environment as it moves in a generally forward direction. This could be achieved by modulating the amplitudes of two output lines, one controlling the right stepper motor and the other controlling the left motor in an alternating fashion. The net effect from the two motors would simultaneously determine the degree of turning and the forward speed of the vehicle.

Getting (1989) describes the simulation of a small CPG network based on the escape swimming control circuit of the mollusk Tritonia diomedea. The methods employed, namely continuous systems modeling, were appropriate for the purpose of explicating some aspects of the mechanisms of a biological network. These were quite different from our own purposes - to emulate behavior with a discrete system model. Nevertheless, certain features of these models and those of adaptrode-based neurons that we had been using to mediate non-adaptive dynamical functions in MAVRIC's brain, suggested the possibility of obtaining behavioral results similar to those inferred from continuous models. We were led to the notion of building a CPG circuit for MAVRIC's motor control using adaptrode-based neurons because of the similarities between the time-course behavior of some synapses (i.e., fast and slow connections) in biological models and that of non-associative adaptrodes having different valued control parameters (Mobus, 1994a). Adaptrodes with slowly or rapidly rising or falling response curves can easily be constructed. Additionally, as noted by Getting (1989), some types of interneurons participating in CPG circuits demonstrate an habituating-like behavior in that they cease firing after some period of continued stimulation even though the stimulus remains. This is modeled in adaptrode-based neurons by using a special adaptrode, the input to which is actually the output of the neuron, to up-modulate the threshold of that neuron so that, after a burst of activity, the neuron's firing rate diminishes and eventually ceases. Using the basic description of the simulated tadpole swimming circuit (Roberts, 1989) we constructed a simple four-cell model CPG (Figure 2).

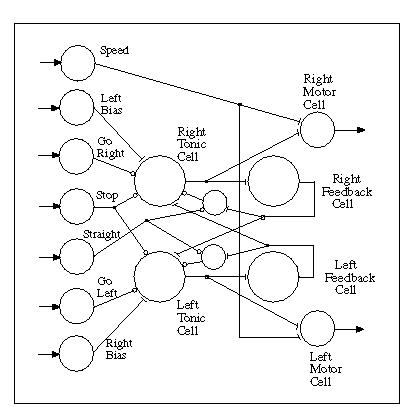
Fig. 2. The Central Pattern Generator (CPG) motor control circuit is comprised of four "core" neurons that generate a quasi-chaotic sinusoidal signal (left motor minus right motor). Additional neurons provide signal distribution for externally applied control signals that are used to modulate and shape the output signals. Pointed arrows indicate signals from/to the external environment. Flat terminals indicate excitatory connections while circular terminals indicate inhibitory ones.

The circuit in Figure 2 reflects the bilateral symmetry of the vehicle and the opponent process used to steer. It is composed of two "tonic" cells, which spontaneously fire at a relatively constant low rate, and two "feedback" cells. In operation the right tonic cell is given a boost in firing rate by an input from the "left bias" neuron (to get things started). In turn, the right tonic cell stimulates the right feedback cell which undergoes a transient increase in it's output . This cell provides inhibitory feedback to the tonic cell, thus dampening its output, but it also provides excitatory input to the left tonic cell, increasing its output. Subsequently, the left tonic cell excites the left feedback cell which inhibits the left tonic cell and excites the right tonic cell, thus starting the cycle over again. Once set in motion, the contralateral excitation, unilateral inhibition cycle will continue indefinitely.

Output from the tonic cells is used to excite the right and left motor cells (these generate the stepper motor pulses) on their respective sides. When the right tonic cell is active (and the left tonic cell is relatively quiet by comparison) the right motor cell generates many more pulses per unit time and thus causes the right stepper motor to rotate faster. This produces a net left turning motion in the robot. Similarly, when the left tonic cell is more active, a right turning motion is made. The net effect of this alternating activity between right and left motor cells is to cause the robot to follow a weaving course, first turning leftward, then rightward, as it moves in a generally forward direction.

Excitatory synapses are implemented using relatively fast-response, slow decay non-associative adaptrodes, while inhibitory synapses are implemented with slow-response, fast decay non-associative adaptrodes. In addition, the threshold of the feedback cells are modulated, slowly, by an adaptrode which gets its input from the output of those cells. The modulation pushes the threshold of the cell lower than its resting level, thus making it easier for the net input to the cell to cause the cell to fire. Since adaptrodes continue to provide a decaying response after the input signal ceases, the effect is to cause the feedback cells to act as bursters. That is, they fire a volley of pulses which continues for a time after the offset of the excitatory input from the corresponding tonic cell. The length of time that this burst continues then determines the time that the corresponding tonic cell will be inhibited and the contralateral tonic cell will be excited. Clearly, the slowness of the inhibitory synapse from the feedback cell to the tonic cell must match the duration of the burst.

Additional inputs to the circuit (shown in Figure 2 as pointed arrows) provide a convenient method of modulating the oscillator in a manner reminiscent of the biological CPGs described above. These inputs are distributed by a layer of neurons which provide a means of overriding, through inhibition (not shown), the effect of the primary signal. The input labeled "Speed" does not directly effect the oscillator circuit. It merely increases the firing rate of the two motor output cells as shown. Other inputs change the form of the output as depicted in the histogram in Figure 3, below. The "Straight" signal can be seen to provide inhibitory input to two cells that supply the inhibitory feedback signal to the tonic cells. This action induces the two tonic cells to become more synchronous leading to a nearly zero net output and the robot moves in a somewhat straight line. When the "Straight" signal is removed or just reduced, the signal returns to its oscillatory behavior with a peak amplitude proportional to the level of the "Straight" signal.

Similarly, the "Go Right" or "Go Left" signals dampen their respective tonic cells which in turn dampens the contralateral excitation feedback. This allows the undamped tonic cell to provide a more or less steady output to its respective motor cell and results in the robot making a smooth and sustained turn. A weaker signal at one of these inputs results in a weaker turning with a small oscillatory wave superimposed.

The "Left Bias" and "Right Bias" signals perform a slightly different function when used. If the "Right Bias" cell is active (it is actually a tonic cell also), the net output signal to the motor cells is essentially the same in form but tends to favor the left motor output. The robot will move in the same weaving pattern but has a tendency to move in a diverging spiral. The capacity to make turns or go straight is not seriously hampered. The modulatory inputs to the CPG circuit come from the cue recognition and direction determining networks of MAVRIC's brain (Mobus & Fisher, 1994).

As originally conceived, this circuit was expected to produce a sinusoidal net output (between left and right motor cells). Indeed, the weaving pattern that the robot followed when run with the new neural oscillator controller was roughly sinusoidal. However we noted certain peculiarities in the pattern. Far from producing a fixed sinusoid, the weave pattern of the robot showed erratic deviations from a sine curve. Sometimes it would make short right or left turns followed by long, sweeping turns. Other times it would make short turns one way and long turns the other causing it to veer dramatically from a given course. Our first conjecture on this behavior was that this was simply the result of slippage of the wheels, a notorious problem in conventional robotics. However, after looking at the pulse counts being sent to the motors it was clear that the erraticness was due to the output of the oscillator. Subsequently we collected and analyzed the raw count data from the oscillator and were surprised to discover that it generated a more complicated signal. As seen in the histogram in Figure 3, the oscillation appears to have a complex waveform.

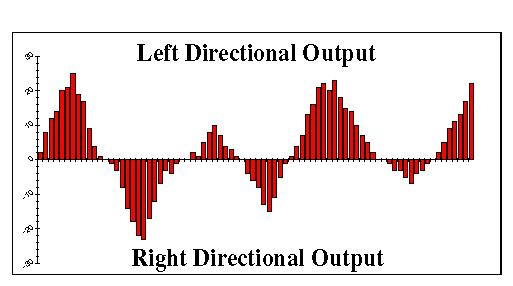
Fig. 3. A histogram of the CPG net (of right and left motor signal) output shows that the direction of the robot varies in a roughly sinusoidal pattern with non-deterministic characteristics of amplitude and wave length. The amplitude of each bar represents the degree of turning that the robot does per second. Negative values represent turns to the right, positive values indicate turns to the left.

Following a suggestion by Bruce West, we decided to look at this data from the perspective of chaos theory. Specifically we undertook to reconstruct the attractor dynamics from a large sample of the time series as shown in the histogram. Figure 4 shows a plot of a two dimensional attractor based on plotting a reconstructed phase space from two points in the time series separated by a specified number of time points, in this case 2. As can be seen in the plot, some kind of non-periodic attractor is associated with the oscillator process. To claim that the system is chaotic, in the sense of deterministic chaos, would be premature from this one form of evidence. However, several observations might be made. First, it is clear that the system is bounded in phase space-hence some kind of attractor is operative. Second, it appears to be the case that the system does not repeat itself; that it is not merely a quasi-random number generator. A final piece of evidence comes from mapping the course taken by the robot (unstimulated by external cues) over a number of runs. This plot (Figure 5), showing divergence as the search time increases, strongly suggests that the path taken is sensitive to initial conditions. We have not pursued a more rigorous analysis of this process with respect to its apparent chaotic nature for the simple reason that it isn't terribly important to our main line of work to show that the oscillator is chaotic in some strict sense. We were seeking a means of getting a robot to scan its environment while it moved, and to that end the oscillator provided a good solution. That it should introduce novelty into the search path was, from our perspective, a bonus. However, the form that this novelty takes, that is in not being a random walk, may have important consequences for the notion of foraging search.

4. RESULTS OBTAINED WITH MAVRIC

Our original objective had been to get MAVRIC to weave as it moved forward so that it would obtain a sensory sweep of its environment. We also required that the motor program allow for easy modulation so that the robot could shift to directed movement gracefully. To those ends the CPG oscillator network produced excellent results. In numerous test runs from a fixed starting point, (home), MAVRIC was able to sense and thus learn a sufficient number of cue-mission events that were placed in its workspace. Subsequent runs showed that MAVRIC was able to locate resources from cue information alone as described in (Mobus & Fisher, 1993; 1994). We had achieved the desired level of autonomy in that MAVRIC no longer needed to be "trained" on specific contingencies in order to succeed in finding its mission resources.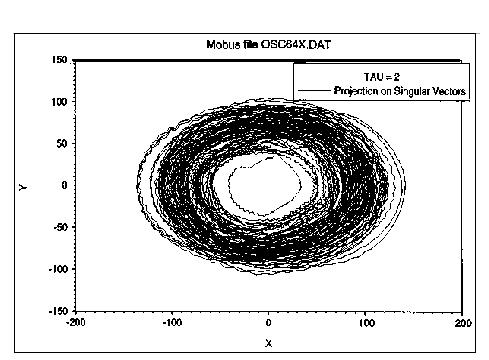

Fig. 4. Plot of a reconstructed, two dimensional phase space showing the attractor dynamics of the CPG oscillator. This plots the behavior in a space defined by two points taken from the time series data as shown in Figure 3. The two points are separated by two time ticks (TAU = 2). This plot was generated from 20,000 data points.

That the oscillator produced a novel search path each time the robot was started from its home did not seem to have any negative consequences[5] for the success of the robot, as had been the case with the random walk novelty scheme. It did not immediately dawn on us that these paths might have a real beneficial impact on the capabilities of the robot.

When thinking about the nature of real world environments we realized that many mission resources occur in stochastic episodes. Certainly the food resources of foraging animals appear and disappear in different locations. There may be a certain amount of regularity in these dynamics, for example, fruit may ripen in a given season or prey animals may always show up at a watering hole. Thus the nature of resource dynamics may, itself, be chaotic, and the timing and quality of the resource are subject to variations that make precise prediction impossible. Because the occurrence and location of resources might be indeterminate, it would be counterproductive for an agent to follow the same path on each iteration of searching. Rather, following a novel path will further ensure that the agent searches a larger volume of the space. Novel search paths would also provide an answer to the problem of occlusion of a resource behind fixed obstacles.

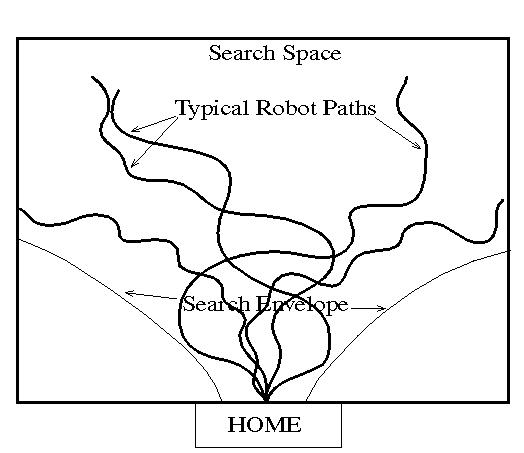
Fig. 5. Examples of typical search paths traversed by MAVRIC show the drunken weave pattern resulting from the OSC output as shown in Figure 2. Also note the apparent bounded nature of the search envelope and the fact that each run takes a novel course.

At the same time, search paths would seem to best be constrained in terms of a general direction. Random walk search, while producing completely novel paths on each iteration, appears to cover too much of the volume. If, as we have speculated, resource dynamics in natural environments follow a chaotic pattern (at least in the general case), then it makes sense that one should constrain the search volume to correspond with the spatial extent of the sought phenomena. A chaotic search pattern would thus provide constrained novelty to match that found in the sought resource.

To do a preliminary test of this notion, we projected part of the trajectory of a Lorenz attractor phase space map onto the plane. A series of points along the trajectory were chosen randomly to represent locations and times for the occurrence of mission-critical events. Within the sensory envelope of the event a second event, called a cue, was defined which would reliably associate with the mission event[6]. The result was that resources (and cues to their presence) appeared stochastically and episodically as the trajectory evolved (Figure 6). MAVRIC was set on a series of iterative searches over the course of this evolution. The figure shows a single mission event and its relationship to the search envelope resulting from the chaotic weave pattern of MAVRIC's motion. Two paths, as shown, lead to finding the resource. The path labeled A shows the result of a coincidental discovery of the resource prior to learning the association between the resource and the cue event (a light source). MAVRIC's course is unaffected by the cue gradient, but as the robot encounters the resource gradient it transitions from the chaotic weave pattern to a gradient following pattern. This transition is effected via the modulation of the CPG oscillator by the directional input, "Straight", as shown in Figure 2. This signal is supplied by a gradient detection network that increases the "Straight" signal in proportion to the difference between two successive samples of the stimulus[7].

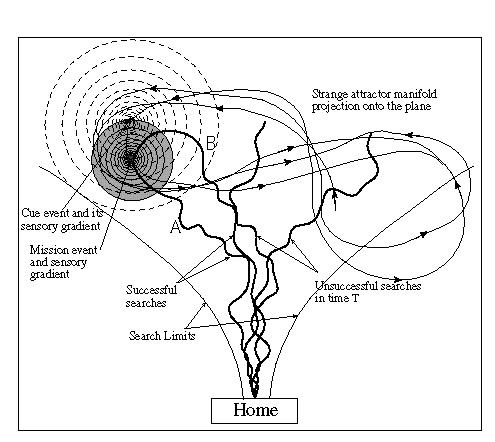
Fig. 6. Experimental layout for MAVRIC to search for a chaotic resource. A common chaotic attractor phase space map has been projected onto the plane of the lab floor. This trajectory is used to place and time the occurrence of resource (mission-critical) events and their associated cue events. Several representative MAVRIC search tracks are shown.

The path labeled B shows a path after learning the association in which MAVRIC follows the cue gradient, by the same mechanism as it follows a resource stimulus gradient, until it encounters the resource gradient, afterwhich it follows the latter to the source. In this model, the learned cue need not be contiguous with the resource object. The extent of the cue field should be greater than that of the resource so that it has the effect of enlarging the latter. Sensing the cue at a greater distance from the resource than it could sense the resource itself, the robot transitions from chaotic wandering and entering the cue field improves its chances of encountering the resource field.

Other paths depicted in the figure would lead to failure. Under additional assumptions regarding the average resource density, several mission (or resource) events might be present in the map of the trajectory at any given time. These would be spaced so that there would be no overlap in the resource gradient fields as detected by MAVRIC.

Thus MAVRIC was set to searching for its mission resources in what we believe represented a natural-like environment. As it had when the resource was set in the same location each time, MAVRIC was able to find its objective in a completely autonomous way, first finding the resource coincidentally and then learning how to improve its results by following the cue gradients that it encountered.

Because of its flexibility and ease of interfacing directional and speed controls with the other parts of MAVRIC's brain, the CPG oscillator proved to be an excellent, if not convenient, approach to solving the motor program problem for this class of robot. The injection of novelty in the absence of directed search has added additional, unanticipated, functionality to the process and, at least from the perspective of our initial experiences, has improved the actual performance of that process.

5. SOME IMPLICATIONS AND OTHER APPLICATIONS

Searching a large, dynamic space for a consumable resource, within time constraints, presents some interesting challenges for robotics and autonomous agents in general. The nature of the dynamism of natural environments should in general be considered at best stochastic and possibly chaotic. This translates into some degree of uncertainty as to the location of the resource each time a search is conducted. In the case of chaotic dynamics, traditional statistical-based prediction is probably inadequate.

Our experience with the chaotic oscillator motor drive network or artificial CPG has led us to consider the role of novelty in generating search paths in the absence of cue-directed searches. Novelty ensures that the search path selected on iterative searches will not lead the agent to the same places each time. In this regard it may be analogous to the use of simulated annealing (SA) to prevent gradient-following algorithms from getting stuck in local minima. Clearly, once a resource has been found at a given location, and consumed, the agent need not return to that location in a subsequent search. The degree of novelty (perhaps analogous to the temperature in SA) is important in that too much results in something like a random walk in which old territory may be explored repeatedly. Not enough results in a relatively narrow envelope of exploration relative to the total space.

That a simple circuit such as the CPG can generate novelty of the "right" form in motor control suggests other possibilities for the role of such circuits in exploration in general. The existence of oscillations in the cortex of vertebrate brains has been established. Is it possible that some of these are sufficiently chaotic to cause novel firing patterns of other neural circuits? Could such circuits give rise to creativity in human mental processing?

One of the cornerstones of human level search in a high dimensional "thought" space is the role of creativity in finding novel paths to a solution. Do we not often "forage" (or hunt) for a solution to a problem? These are, of course, highly speculative musings and clearly far beyond the realm of investigating intelligent behavior in snail level artificial agents. However, such speculations may prove to be useful guides in exploring brain architectures for more complex robots in the future.

In the meantime, we have begun to think of the method of foraging, in the sense of coupling a chaotic path generator with a learning mechanism, as a solution to search problems in discrete domains such as computer memories. Exhaustive search of a discrete space, as represented, say, by a graph, is not overly burdensome, computationally, in that it is known to scale linearly with the number of nodes and edges. However, the problem of searching a large space for dynamically changing resources (graph labels) can be problematic if the rate of change in the labeling or topology of the graph is greater than the time needed to conduct the search. If one views the combined memory space of all computers tied into the Internet, for example, as a vast, dynamic search space, then it is possible that the method of foraging search may be brought to bear. We are thus beginning to look at the extrapolation of the methods that have proven useful in our physical robotics application to the cyberspace environment afforded in the Internet. Here a "knowbot" agent, or software robot, (Etzioni & Weld, 1994) might forage through the network, looking for resources, such as documents containing specific key phrases. It could use the names of computers and files (or gopher menu components) as potential cues, learning cue words that increase the likelihood of finding the sought documents over repeated searches. It will be interesting to explore the notion of a chaotic oscillator in such an architecture.

6. ACKNOWLEDGMENTS

We would like to thank Manny Aparicio for his contributions to this work in discussions and collateral work with Mobus on foraging search in animals. We would also like to thank Bruce West for his suggestions and guidence in reconstructing the dynamic behavior of the oscillator.

REFERENCES

Alkon, D. L. (1987). Memory Traces in the Brain. New York, NY: Cambridge University Press.

Braitenberg, V. (1984). Vehicles: Experiments in Synthetic Psychology. Cambridge, MA: The MIT Press.

Brooks, R. A. (1991). Intelligence without reasoning. Technical Report A.I. Memo No. 1293. Cambridge, MA: MIT Artificial Intelligence Laboratory.

Durbin, R., Miall, C. & Mitchison, G. (Eds.), (1989). The Computing Neuron. New York, NY: Addison-Wesley Publishing Co.

Etzioni, O. & Weld, D. (1994). A softbot-based interface to the internet. Communications of the ACM, 37,7, 72-76.

Getting, P. A. (1989). Reconstruction of small neural networks. In C. Koch & I. Segev (Eds.). Methods in Neuronal Modeling: From Synapses to Networks. (pp. 171-194). Cambridge, MA: The MIT Press.

Kleinfeld, D. & Sompolinsky, H. (1989). Associative network models for central pattern generators. In C. Koch & I. Segev (Eds.). Methods in Neuronal Modeling: From Synapses to Networks. (pp. 195-246). Cambridge, MA: The MIT Press.

Koshland, D. E. (1980) Bacterial Chemotaxis as a Model Behavioral System. New York, NY: Raven Press.

Mackintosh, N. J. (1983). Conditioning and Associative Learning. London, England: Oxford University Press.

Mobus, G. E. (1994a). A Multi-Time Scale Learning Mechanism for Neuromimic Processing. Ph.D. Thesis, Unpublished. Denton, TX: University of North Texas.

Mobus, G. E. (1994b). Toward a theory of learning and representing causal inferences in neural networks. In D. S. Levine & M. Aparicio (Eds.), Neural Networks for Knowledge Representation and Inference, (pp. 339-374). Hillsdale, NJ: Lawrence Erlbaum Associates.

Mobus, G. E. & Fisher, P. S. (1991a). Conditioned response training of robots using adaptrode-based neural networks I: Continuous adaptive learning. In G. Mesnard & R. Swiniarsk (Eds.) Proceedings of the International AMSE Conference on Neural Networks. (pp. 171-182). San Diego, CA: Association for the Advancement of Modeling and Simulation Techniques in Enterprises.

Mobus, G. E. & Fisher, P. S. (1991b). Conditioned response training of robots using adaptrode-based neural networks II: Simulation results. In G. Mesnard & R. Swiniarsk (Eds.) Proceedings of the International AMSE Conference on Neural Networks. (pp. 183-194). San Diego, CA: Association for the Advancement of Modeling and Simulation Techniques in Enterprises.

Mobus, G. E. & Fisher, P. S. (1993). A mobile autonomous robot for research in intelligent control. Technical Report CRPDC-93-12. Denton, TX: Center for Research in Parallel and Distributed Computing, University of North Texas.

Mobus, G. E. & Fisher, P. S. (1994). MAVRIC's Brain. In F. D. Anger, R. V. Rodriguez, & M. Ali, (Eds.), Proceedings of the Seventh International Conference, Industrial and Engineering Applications of Artificial Intelligence and Expert Systems (pp. 315-322). Yverdon, Switzerland: Gordon and Breach Science Publishers.

Roberts, A. (1989). A mechanism for switching in the nervous system: turning on swimming in a frog tadpole. In R. Durbin and C. Miall and G. Mitchison (Eds.), The Computing Neuron. (pp. 229-243). New York, NY: Addison-Wesley Publishing Co.

Selverston, A. & Mazzoni, P. (1989). Flexibility of computational units in invertebrate cpgs. In R. Durbin and C. Miall and G. Mitchison (Eds.), The Computing Neuron. (pp. 205-228). New York, NY: Addison-Wesley Publishing Co.

Footnotes:

1 This follows from the "Darwinian" argument that were they not successful, they would not survive. [back to text]

2 Here we are using the word in the sense of organized uncertainty, as in deterministic chaos. The world is organized within broadly determined "laws" but, owing to nonlinear interactions and lack of precision in determining initial conditions, becomes less predictable as the time horizon lengthens. [back to text]

3 In our system, a cue is a sensory gradient that extends over a much wider area than the sensory gradient of the resource object, for example, a visual cue (the sight of a landmark) may be seen from a greater distance than the scent of food.[back to text]

4 The temporal ordering observed is generally strict and requires that the primary signal arrives some time prior to the arrival of the secondary signal. The time interval required depends on the time-domain level being gated. In the case of gating the transfer of the short-term memory trace into the intermediate-term trace this may only require a few time steps. The ordering, however, ensures that a proper causal correlation is encoded. [back to text]

5 Ironically, we spent a fair amount of time trying to smooth out the erraticness of the oscillations without increasing the complexity of the circuit - to no avail. Eventually, after seeing that the novel paths did not reduce the robot's ability to find resources, we decided to let well enough alone. [back to text]

6 Typical mission events would be the sounding of a specific tone the volume of which was varied to represent the gradient field. A cue event was the placement of a light near the speaker. The light would be dimmed so that MAVRIC had to be within a certain distance before it could detect the light. [back to text]

7 This strategy emulates the tumbling search mechanism in swimming bacteria reported by Koshland (1980). [back to text]

Back to George Mobus' Home page.