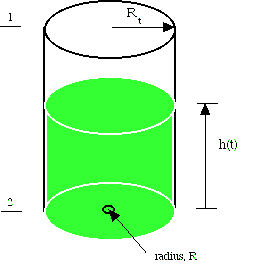
Tank Drainage Derivation
Consider the tank problem illustrated in the figure. The tank drains, but as the height gets smaller, it drains more slowly. This problem can be solved by using a macroscopic mechanical energy balance and mass balance, following Bird, et al.(ref). The mass balance is
The term m
tot is the total mass of the system, and
is the mass flow rate in or out of the system and <v> is the average velocity, averaged over a cross section of the inlet or outlet. The mechanical energy balance is
where the terms represent the time variation of the kinetic energy of the system, the time variation of the potential energy of the system, and the difference between the inlet to the outlet of the kinetic energy, potential energy, and pressure energy. K
tot is the total kinetic energy of the system, and Ftot is the total potential energy of the system. The terms on the right hand side are differences from the inlet to the outlet; the Æ terminology is positive going out and negative going in. The balance is made over a control volume which includes the air above the fluid down to the hole. The terms are: <v3> is the velocity to the third power, averaged over the area of the inlet or outlet,
is the potential energy per unit mass, or the acceleration of gravity times the height above some datum, p is the pressure, and r is the density. The potential energy change from the inlet to outlet is small because the potential energy at the bottom is zero and the potential energy of the air above the fluid is negligible. The pressure in and out is the same, since both ends of the tank are exposed to essentially the same pressure, there is no work, and for this balance the compression work and viscous dissipation are neglected. Under these conditions, Eq. (2) reduces to
The terms are evaluated for the case of a constant velocity profile, i.e. the velocity does not vary in the direction transverse to itself. The mass balance becomes
The kinetic energy term is
where R is the radius of the small hole at the bottom, R
t is the radius of the cylinder above, h is the height of the fluid in the cylinder, and v2 is the velocity out the hole. The kinetic energy of the system that changes in time is due to the velocity of the upper surface of fluid; while the velocity varies with time in the small hole, it does so in an infinitesimal volume and doesn’t contribute to the integral. However, continuity is used to express the kinetic energy involving the velocity at surface 1 in terms of the velocity at surface 2.
The potential enegy of the system is
When the velocities are considered constant across the tubes, the kinetic energy term is
(Recall that the top surface is in air, and the density and velocity are very much smaller than those in the fluid at the outlet). Combining all terms gives
Divide Eq. (4) by
r p R2 / 2 to get
Likewise, the mass balance is
Bird, et al.(ref) manipulate this equation by rearranging Eq. (1) to solve for velocity
and substituting into Eq. (5). The final result is
This is a second order equation, which is an initial value problem. The initial conditions are that
The so-called Torricelli’s velocity is
Eq. (6) can be integrated analytically, but the result is cumbersome (ref). It can also be integrated numerically as an initial value problem. One defines
and then integrates the two initial value equations
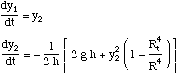
The initial conditions are.
Solution method (link)
As a variation of this problem, consider the case when there is a straight length of pipe at the exit.
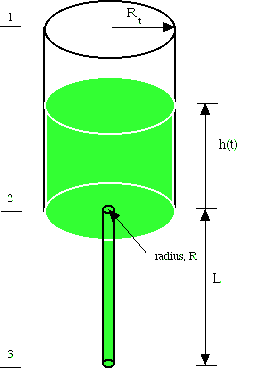
Now there is viscous dissipation in the pipe. The mechanical energy balance now has additional terms on the right-hand side.
The viscous dissipation for the contraction is usually expressed as
where e
v is a constant depending on the contraction ratio.
The viscous dissipation in the straight pipe is
where f is the friction factor. Now the mechanical energy balance is
where f(v
2), although it may be assumed constant over some time period. After dividing by r p R2 / 2 we get
Continue on to solve the problem.