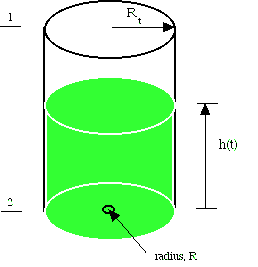
Consider the tank problem illustrated in the figure. The tank drains, but as the height gets smaller, it drains more slowly. This problem can be solved by using a macroscopic mechanical energy balance and mass balance, following Bird, et al.(ref). A complete derivation is given in another panel. (link)

The mass balance is

is the mass flow rate in or out of the system and <v> is the average velocity, averaged over a cross section of the inlet or outlet. The mechanical energy balance is

These terms are evaluated (link) and the equations rearranged to give the following single equation of second order.

This is a second order equation, which is an initial value problem. The initial conditions are that

The so-called Torricelli’s velocity is

Eq. (6) can be integrated analytically, but the result is cumbersome (ref). It can also be integrated numerically as an initial value problem. One defines

and then integrates the two initial value equations

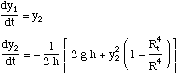
The initial conditions are.

Rather than doing that, we prefer to solve for the height and velocity. Let

The mass balance then becomes

while the mechanical energy balance becomes

After rearrangement this becomes

We can solve these equations with the initial conditions

Case (a) will give the same solution as the second order equation in h. Case (b) is for an initially quiescent fluid. In addition, we can solve the problem with the time derivative of the kinetic energy ignored, since we expect it to be small. In that case the problem is (case c)

These three problems are solved together in the code (link). The figure shows the height as a function of time. Since the three models give almost identical results, the solutions are plotted with an offset for clarity. Indeed it looks like the solutions are the same, but they aren’t.

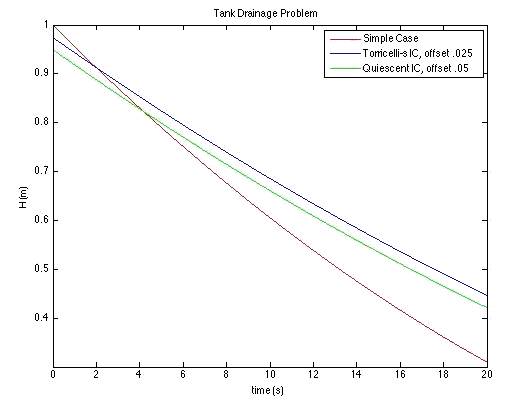
The velocity for case (a), Torricelli’s initial condition, is the value that would ultimately be achieved at steady state. Due to the terms in the equation (particularly the ratio of radii) this velocity is achieved extremely rapidly whenever h changes. The velocity at the initial time is essentially constant in the figure, since the height hasn’t changed much in the first 0.04 seconds. The velocity for case (b), though, is zero initially, and it quickly increases to the Torricelli velocity, as seen in the figure. This figure illustrates the fact that the Torricelli velocity is achieved very quickly whenever h changes. This justifies the neglect of the kinetic energy term, which then makes the problem very simple, case (c).

As a variation of this problem, consider the case when there is a straight length of pipe at the exit.

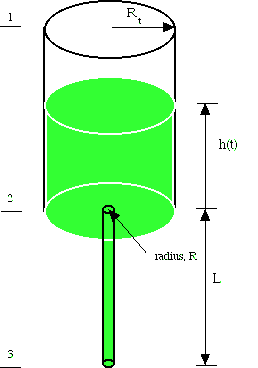
Now there is viscous dissipation in the pipe. The mechanical energy balance is changed to (link)

The solution to this problem is similar to what was done above, as long as one assumes that the friction factor is constant. This won’t be strictly true, since the velocity changes with time, and hence the Reynolds number changes, too. This variation could also be included; in this case an analytical solution is unlikely without assuming a constant friction factor.

Take Home Message: Sometimes terms in the equations can be neglected, making the problem much simpler. If all terms are included, the solution may be stiff since one component of the solution may vary extremely rapidly to its quasi-static value.