What is a stiff set of equations?

What makes a set of ODEs stiff?

To understand what makes one set of ordinary differential equations more difficult to solve than another, we need to understand how quickly each of the equations moves towards its own steady state solution.

For instance, if we have a set of ODEs that describes how the mole fraction of a component in a system and temperature of the system change with respect to time, we could try to solve them as a system of equations.

[Next] Back to ODE Page

However, if the mole fraction changes very rapidly and the temperature takes much longer, we must integrate the two equations using very small steps to catch what is going on with the mole fraction, while integrating for a long time to establish what the temperature is doing.

It is this fact, that one of the parameters changes quickly and the other changes slowly, that makes the set of equations stiff.

[PREV] [Next] [TOP] Back to ODE Page

Here is how to determine if a set of differential equations is stiff.
The two equations below are a simplified model for a catalytic converter, where y denotes the mole fraction of CO in the gas phase and T denotes the temperature of the gas phase. The model was simplified by excluding the reaction term.

[PREV] [Next] [TOP] Back to ODE Page

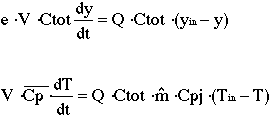
When the constants are substituted into the above equations we get:


By solving for the eigenvalues for this system of equations, we can tell which variable, y or T, is going to its steady state solutions faster. Note.

[PREV] [Next] [TOP] Back to ODE Page

For information regarding eigenvalues for systems of ODE's, please consult an ordinary differential equations text.

[PREV] [Next] [TOP] Back to ODE Page

It is the ratio of the eigenvalues (larger over smaller) that tells us if the equations are stiff. A ratio of 1000 qualifies as 'stiff', while a ratio of 5000 would be 'very stiff'.

[PREV] [Next] [TOP] Back to ODE Page

Here is the ratio of the Eigenvalues.

[PREV] [TOP] Back to ODE Page

Page constructed by

Doug Thornhill, James Bopp, Cory Clemmons and Devin Hodgson.

For questions or suggestions, please contact us through dt@u.washington.edu
Last modification on 7 Dec 95.