This page is intended to illustrate for proportional controllers:
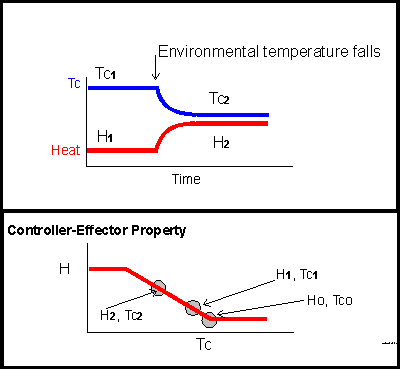
The upper panel of the graphic illustrates two equilibrium temperatures: first a constant temperature Tc-one that is maintained by a constant level of heating, H-one, then, after a change in the environment, a transition to a new equilibrium at a lower temperature, Tc-two, associated with an increased level of heating, H-two. This could represent, for example, the thermal behavior of a heated laboratory water bath equipped with a proportional controller. In a relatively warm environment, little heat is called for; if the environment cools, the consequent tendency for bath temperature to fall causes increased heater output.
 <>
<>
Without a temperature controller, temperature inside the bath would simply follow environmental temperature. It would be higher than environmental temperature if the heater were set at a fixed level, but would equilibrate at a fixed increment above environmental temperature. With heater output adjusted by a proportional controller, temperature inside the bath still follows environmental temperature but bath temperature changes less than environmental temperature. How much less depends upon the proportionality between bath temperature and heater output. This proportionality, the slope of the line in the lower panel of the graphic, is called the gain of the controller. The bigger the gain, the greater the increment in effector output for a given change in sensed temperature.
The equilibrium points corresponding to the steady temperatures in the upper panel are circled. Had the slope of the controller relationship been steeper, the higher heat level, H-two, would have been reached before temperature fell to Tc-two; in other words, the steeper the slope, the better the regulation. In the real world, this is complicated by the fact that making the gain of a system too high is likely to cause it to oscillate because of the lag in time between application of heater power and achievement of a stable temperature in the controlled medium.
To be specific about the equilibrium following the change in environmental temperature illustrated in the graphic -- what determines the new equilibrium is the controller property in relation to the additional load imposed by the environment. On the lower panel, the equilibrium point at H-two and Tc-two is circled. At this point, the heat output level set by the controller (H-two) matches the rate at which escapes from the system. That rate of heat loss is driven by the difference between temperature inside the system, Tc-two, and temperature outside. Temperature remains constant at Tc-two because the rate of heat output set by Tc-two is exactly the right rate to balance the heat loss driven by the gradient between Tc-two and outside temperature.
Each of the two equilibrium points here, Tc-one and Tc-two, is at a temperature offset from Tc-zero. The amount of the offset is called the error signal. The bigger the thermal load imposed by the environment, the bigger the error signal, sometimes called the load error. If we think of Tc-zero as the set point, then the load error is the difference between the equilibrium temperature and the set point.
These terms are used in discussions of human temperature regulation. For example, the elevated core temperature maintained during exercise has been described as representing a load error. You have to have this elevated temperature to activate the physiological defenses.
Finally,the change in equilibrium temperature from Tc-one to Tc-two illustrated here is obviously not due to a change in set point. Nothing in the controller properties changed, only the equilibrium temperature and heater output. Probably no one would make the mistake of interpreting an observed change in equilibrium temperature as due to a change in set point in a situation like this where it was clear that the change in environmental conditions disturbed the initial equilibrium.
It is when equilibrium temperature changes under fixed enviromental conditions (for example, when temperature falls in a supine human around the time of sleep onset) that people are likely to say "Aha, the set point has changed". Maybe so. The next page. illustrates what happens to equilibrium temperature in a simple proportional control system when the set point is altered.
However, the same change in eqilibrium temperature can equally occur as a consequence of altered gain. That is illustrated in the final page on simple proportional control systems, linked from the next page and the index page.