Lab 4
We will consider forward substitution and an iteration scheme for linear systems.
Contents
Exercise 1: Forward substitution
Let  be an
be an  lower triangular matrix with non-zero diagonal entries. We want to solve
lower triangular matrix with non-zero diagonal entries. We want to solve

More explicitly:
![$$\left[\begin{array}{cccccccc} l_{11} & 0 & 0 &0 & \cdots & 0 \\ l_{21} & l_{22} & 0 & 0
& \cdots & 0 \\ l_{31} & l_{32} & l_{33} & 0 & \cdots & 0 \\ \vdots & &&&& \vdots \\
l_{n1} & l_{n2} & \cdots && \cdots & l_{nn}\end{array}\right] \left[ \begin{array}{c} x_1 \\ x_2 \\ \vdots \\ \vdots \\ x_n \end{array} \right] = \left[ \begin{array}{c} b_1 \\ b_2 \\ \vdots \\ \vdots \\ b_n \end{array} \right].$$](Lab4_eq09051131375968397943.png)
This gives the set of equations
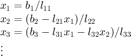
And in general
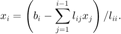
Given an augmented matrix, ![$[L,b]$](Lab4_eq15594683397315749802.png) implement the forward substitution algorithm to solve
implement the forward substitution algorithm to solve  , call your function
, call your function
Forsub()
Test your algorithm on a matrix  given by
given by
n = 10;
L = rand(n); b = rand(n,1);
for i = 1:n
for j = i+1:n
L(i,j) = 0;
end
endExercise 2: An iterative solution
Define matrix 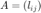 for any dimension
for any dimension  by
by
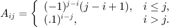
Define  to be the lower-triangular part of
to be the lower-triangular part of  , and
, and 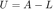 . If you want to solve
. If you want to solve 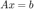 you can consider
you can consider 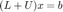 ,
,  . The solution
. The solution  is a fixed point of
is a fixed point of 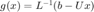 .
.
Use your forward substitution algorithm (and not compute the inverse of L!) and fixed-point iteration to solve for  when
when  is a vector of all ones. Examine the convergence of the method using
is a vector of all ones. Examine the convergence of the method using
max(abs(x-y))
which returns the maximum entry (in absolute value) of the difference 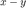 .
.