Lab 2
This lab will be mostly focused constructing more and more complicated functions to handle tasks that need to be repeated.
Contents
Evaluating the exponential function
Consider the Taylor series expansion for  about
about  :
:
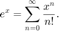
The absolute error for partial sums is given by
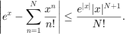
Exercise 1
Write a function exp_frac(x) to compute the exponential function to a relative accuracy of 10e-15 for 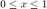 .
.
Create a plot of the absolute and relative error as  increases. Use the semilogy() command to help with this visualzation.
increases. Use the semilogy() command to help with this visualzation.
Exercise 2
The exponential function has the important property that 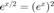 . Construct a function exp_series(x) to compute the exponential function for any number
. Construct a function exp_series(x) to compute the exponential function for any number  using exp_frac(y) where
using exp_frac(y) where 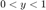 and
and 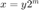 for some
for some  .
.
Create a plot of the absolute and relative error as  increases. Use the semilogy() command to help with this visualzation.
increases. Use the semilogy() command to help with this visualzation.
Exercise 3
Write a function bisection(f,a,b,TOL,Nmax) to find the root of a function f.
Exercise 4
Write a function log_bisect(x) to compute the natural logarithm of 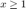 using your exp_series() and bisection() functions. What challenges do you encounter?
using your exp_series() and bisection() functions. What challenges do you encounter?