Computer Assignment 8 (project)
Due Thursday, Dec 1 at 11:59pm
This final computer assignment should be completed ON YOUR OWN. You may discuss the problems with your classmates but the final version must be your own work. We will not hesitate to give zero points for an assignment if it is not your own work.
The assignment MUST be published as ONE .pdf file. The m-files you use should be put in a .zip archive. Your final submission should then consist of one .pdf file and one .zip file. This is worth 50% of your lab grade. Even if you use the m-files that are provided as solutions in the class, they should be turned in. You must also describe where you got the code you use. Stock MATLAB® implementations of the main algorithms in the course can ONLY be used to check your results.
Contents
Problem 1: The inverse power method
Assume the eigenvalues of an  matrix
matrix  satisfy
satisfy

The inverse power method is used to compute 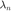 , the smallest eigenvalue of
, the smallest eigenvalue of  .
.
Write a function
InvPower(A,Nmax,TOL)
that performs the following:
1. Compute a 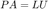 factorization of
factorization of  using partial pivoting.
using partial pivoting.
2. Let 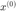 be a randomly generated unit vector.
be a randomly generated unit vector.
3. For  do 4-6
do 4-6
4. Define 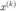 by
by 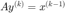 . Solve for
. Solve for 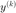 using the
using the 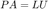 factorization in the following way:
factorization in the following way:
Set 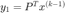 .
.
Solve  with forward substitution.
with forward substitution.
Solve 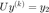 with backward substitution.
with backward substitution.
5. Set ![$\lambda^{(k)} = [y^{(k)})^Tx^{(k-1)}]^{-1}$](HW8_project_eq05612476750061851836.png) .
.
6. Set 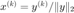 .
.
6. If 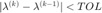 then return
then return 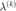 .
.
7. If 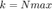 return an appropriate error message.
return an appropriate error message.
Apply this method to the matrix
A = [-2 1 0 0 0; 1 -2 1 0 0; 0 1 -2 1 0; 0 0 1 -2 1; 0 0 0 1 -2];
How many iterations do you need when 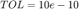 ?
?
Problem 2: Relaxation for fixed-point iteration
Consider finding the fixed-point of the function

Consider using the relaxation iteration
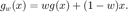
If  is the fixed point, we'd like to choose
is the fixed point, we'd like to choose  so that
so that 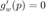 so that we get quadratic convergence, but of course,
so that we get quadratic convergence, but of course,  is not known. The relaxation parameter
is not known. The relaxation parameter  does not need to be the same at each iteration. At each iteration, to compute
does not need to be the same at each iteration. At each iteration, to compute 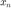 , find
, find  by setting
by setting 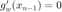 .
.
Implement this method to compute the fixed point of 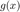 . Show either numerically or analytically that this method converges quadratically.
. Show either numerically or analytically that this method converges quadratically.
Problem 3: The modified Gram-Schmidt process
Implement the modified Gram-Schmidt process to compute a QR factorization of an invertible  matrix
matrix  . Call your function
. Call your function
QR(A)
Demonstrate clearly that your method works on the matrix
A = [-2 1 0 0 0; 1 -2 1 0 0; 0 1 -2 1 0; 0 0 1 -2 1; 0 0 0 1 -2];