Formulas for Estimating the Slope

We first present and explain the conceptual formula for the slope. Then we derive other equivalent forms for the slope that might be more useful for performing calculations. Finally, we show there there is a close relationship between the slope and the correlation coefficient.

Conceptual Formula for Slope

Each observation votes for the slope. The best-fitting line must go through the mean for both variables, so the best slope for any observation is a line passing through both the observation's point and the point defined by the two means. That is, each observation's vote is

We are more confident in the slopes estimated by points far from the mean of X. It turns out that our confidence is proportional to the squared distance of the observation from the mean of X in the horizontal direction. That is, each observation's weight is proportional to:

Dividing this term by the sum of all the squared distances ensures that the average weight will be 1/n. These weights, which must sum to 1, are equal to: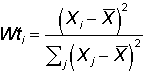

The best estimate of the slope is not the simple average of all the slope votes, but rather the weighted average. That is, the best estimate of the slope is

The first term in brackets is each observation's weight, based on its squared distance from the mean of X, and the second term in brackets is each observation's vote for the best slope.

Alternative Formulas for Calculating the Slope

While the formula above for the slope is conceptual, it is also somewhat unwieldy. A few derivations will produce formulas expressed in more convenient terms. Start with the conceptual expression for the slope:

Cancelling the term

from the numerator of the weight and the denominator of the slope gives the somewhat simpler expression:

Dividing both the numerator and denominator in this expression by (n-1) yields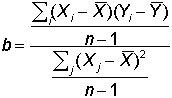

However, the numerator is now by definition the covariance and the denominator is the variance of X; so, the formula for the slope reduces to the simple expression: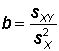

That is, the best estimate of the slope is simply the covariance between X and Y divided by the variance of X.

Relationship to Correlation

The correlation coefficient was also expressed in similar terms as

which suggests there is a close relationship between the slope and the correlation coefficient. Indeed, start with the covariance and variance expression for the slope: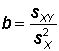

and then multiply both the numerator and denomiator by the the standard deviation of Y to get: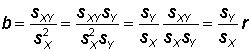

In other words, the slope equals the correlation multipled by the ratio of the two standard deviations. If the correlation coefficient and the two standard deviations have already been calculated, this is a very easy formula for calculating the slope. It is also easy to turn this expression around to calculate the correlation coefficient if the slope and the standard deviations are known. That is,

Move the line up and down by dragging the box or change the slope by clicking and dragging anywhere else so that the line represents all the observations. Try to place the line so that it is closest to all the observations.

Based on your line, do you think there is a positive, negative, or no relationship between SqFt and Market?

Engineering

Test	1	2	3	4	5	6	7	8	9	10
Stress	2.5	5	10	15	17.5	20	25	30	35	40
FailTime	63	58	55	61	62	37	38	45	46	19

Based on your line, do you think there is a positive, negative, or no relationship between Stress and FailTime?

Biology

Based on your line, do you think there is a positive, negative, or no relationship between Age and Reduce?

Participant	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Age	45	43	46	49	50	37	34	30	31	26	22	58	60	52	27
Reduce	30	52	45	38	62	55	25	30	40	17	28	44	61	58	45