Distribution of the Regression Slope
To determine whether particular values for regression slopes are surprising or not,
we need to know the distribution of those slopes. Below we derive various characteristics
of the distribution of the regression slope.
Formula for the SlopeEarlier we derived an equation for the slope as the weighted average of each individual point's slope "vote." That is,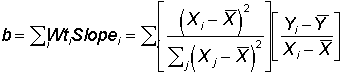
For purposes of deriving the variance and other purposes, it is convenient to reexpress this conceptual formula in simple mathematical terms. Cancelling the common term from the numerator of the first braceted term and the denominator of the second yields: 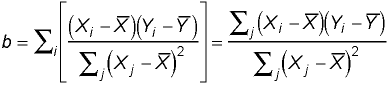
To simplify this expression further, consider the numerator 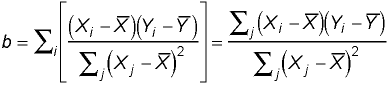
The last term in this expression equals zero; that is, because the definition of the mean requires Substituting the simpler form of the numerator in the formula for the slope gives: 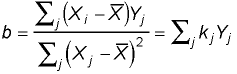
In other words, the slope is simply a weighted average of the original data values where the weight is given by: 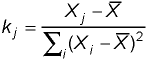
The important point is that the slope is a weighted average or weighted mean of the data values. Thus, according to the Central Limit Theorem, it will tend to have a normal distribution itself. The mean of that normal distribution is the true value of the regression slope. Next we turn to deriving the variance of that normal distribution. Variance of an ObservationAccording to the regression model, each observation isVariance of the SlopeThere are two important properties of the variance are that are needed to derive the variance of the slope. First, the variance of the sum of independent or uncorrelated random variables equals the sum of their variances; that is,Second, the variance of a constant times a random variable equals the constant squared times the variance; that is, For each value or level of X, each individual observation The Y.X subscript indicates that it is the variance of Y when we know X. Applying the rules for sums of variances to the variance of slope expressed as a weighted average yields: The sum of the squared weights can be reexpressed as 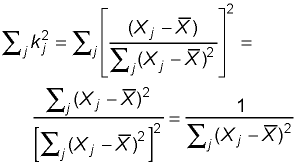
Further note that the denominator is the key term in computing the variance of X; that is, 
This allows expression of the sum of the squared weights as 
Substituting into the equation for the variance of the slope yields the simple expression of that variance in terms of the variance of the data variable, the variance of the predictor variable, and the number of observations. 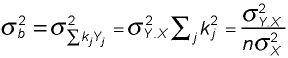
|
||
|
File: © 1999, Duxbury Press. |