File: jmfuns.rda
beta.parameters takes pairs of parameters that are sufficient to determine a beta distribution and computes other parameters that are also sufficient to determine the beta distribution. The possible pairs are (a, b), (mu, kappa), (mode, kappa) and (mu, var). Specifying any one of these pairs returns the values for the other pairs.
beta.parameters = function(
a = NA, b = NA,
mu = NA, mode = NA,
kappa = NA, var = NA,
quantiles = c( 0.10, 0.50, 0.90 ) )
a, b The a and b parameters of the beta distribution (sometimes called alpha and beta, or α and β).
mu The mean of the beta distribution.
mode The mode of the beta
distribution.
kappa The size of the beta distribution.
var The variance of the beta
distribution.
quantiles Quantiles of the beta
distribution. The default value is c(
0.10, 0.50, 0.90
) )
DETAILS:
The input to beta.parameters should be one and only one pair of parameters that are sufficient to specify a beta distribution. These pairs are:
a and b
mu and kappa
mode and kappa
mu and var
beta.parameters will return the values of all of these parameters that can be inferred from the specified values. In addition, it returns the specified quantiles of the beta distribution. Set quantiles = NULL to omit the quantiles.
The results are based on the relationships:
Given
a and
b: mu
= a/(a+b); kappa = (a+b); mode
= (a-1)/(a+b-2);
var = (a*b)/ ( ((a+b)^2) * (a+b+1) )
Given
mu and
kappa: a =
(kappa * mu); b = (kappa - a); mode
= (a-1)/(a+b-2); var =
(a*b)/ ( ((a+b)^2) * (a+b+1) )
Given mode and kappa: a = (mode *(kappa - 2) + 1 ); b = (kappa - a); mu = (a/(a+b)); var = (a*b)/ ( ((a+b)^2) * (a+b+1) )
Given
mu and
var: a =
(((1-mu)/var) - (1/mu) ) * mu^2; b
= a * ((1/mu) - 1); mode = (a-1)/(a+b-2); kappa = (a+b)
Given
mu and var: a = 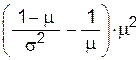 (same as above but easier to
read)
(same as above but easier to
read)
b
= 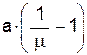
#-------------- The 'doc' bookmark highlights all of the documentation but not the function skeleton at the top of the file. Use rdocToString macro to convert documentation to an R string variable. Bkmk docStringsLoc = <\r\fns\docStrings\>. ---------------
Format for this html document: Page Size = Tabloid:
11" x 17". Note that Tabloid page size is available if Adobe
PDF is set as the default printer, but not if the default printer is a physical
printer that prints 8.5" x 11" standard paper. Table widths =
9.5". Document Screen Width (bk = SetDocScreenWidth): ##120##
#-------------------------------------------------------------