
Planck Version (2013)

Temperature variations of the cosmic background radiation as measured by Planck. Red indicates high temperature and blue low temperature.
I'm a Professor
Emeritus of Physics at the University of
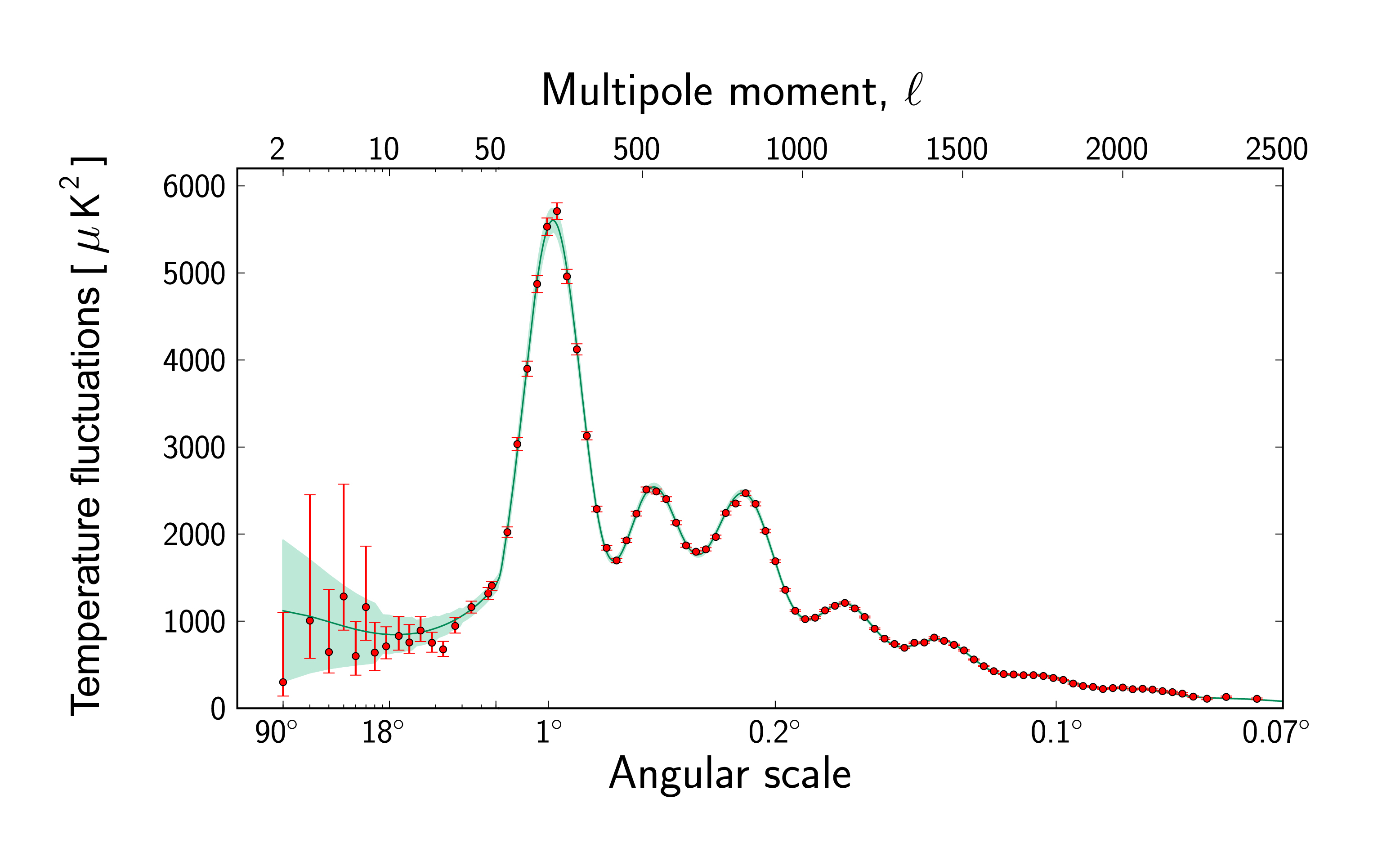
It was not as easy to use the data this time because, while the WMAP group provided an easy-to-find table of multipole strengths from their analysis, the Planck group has set up an arcane system of data archives and ".fit" files that, after several hours of effort, I was not able to penetrate to obtain the data I wanted. Finally, with the help of Dr. Richard Gass of the University of Cincinnati, who provided a sample notebook and advised upgrading from Mathematica 8 to Mathematica 9, I was able to extract the Planck multipole data, which is plotted above and included below as a .txt file.
The Sound of the Big Bang simulation includes three important effects: (1) The multiply peaked frequency spectrum measured by Planck is made into a single sound wave (monaural, not stereo) by the process described above; (2) According to the Planck analysis, the emission profile of the cosmic background radiation peaked at 379,000 years and dropped to 60% intensity at 110,000 years before and after the peak emission time. The simulation represents the first 760,000 years of evolution of the universe, as the emitted CBR rises and falls in intensity following the Planck profile; (3) The universe was expanding and becoming more of a "bass instrument" while the cosmic background radiation was being emitted. To put it another way, the expanding universe "stretches" the sound wavelengths and thereby lowers their frequencies. To account for this effect, the program shifts the waves downward in frequency to follow the expansion in the first 760 thousand years of the universe. How fast the universe initially expanded depends on what cosmological model is used. I decided to follow the predictions of the flat-space Robertson-Walker metric with zero cosmological constant. That model predicts that the radius of the universe grows as time to the 2/3 power (R ~ t2/3). Therefore, instead of the component sine waves varying as (frequency ´ time), they vary as (frequency ´ time1/3) to implement the cosmological Doppler shift. The sound frequencies used in the simulation must be scaled upward by a huge factor (about 10 to the 26 power) to match the response of the human ear, because the actual Big Bang frequencies, which had wavelengths on the order of a fraction of the size of the universe, were far too low to be heard by humans (even had any been around).
I made .wav files from the simulation with playing-time duration of 20, 50, 100, 200, and 500 seconds. These may be downloaded here, along with the Mathematica notebook that produced the .wav files and the data file of the Planck multipole spectrum:
I recommend the 100 second version, but you can choose for yourself. These audio files can be downloaded and used for any purpose, provided the text "(c) John G. Cramer - 2013" is used in text related to the file. References to my website, my Analog Columns, and my two hard science fiction novels Twistor and Einstein's Bridge are also encouraged and would be appreciated.
John G. Cramer
April 14, 2013