
Slide 1
LIS 570
Summarising and presenting data - Univariate analysis
Slide 2
Summary
Basic definitions
Descriptive statistics
Describing frequency distributions
shape
central tendency
dispersion
Slide 3
Selecting analysis and statistical techniques

Slide 4
Basic Definitions
|
|
Values : the categories developed for a variable |
Nominal
Ordinal
Interval
Data : Observations (Measurements) taken on the units of analysis
Slide 5
Basic definitions
Statistics - Methods for dealing with data
|
|
Descriptive statistics |
summarise sample or census data
Inferential statistics
Draw conclusions about the population from the results of a random sample drawn from that population
Slide 6
Methods of analysis (De Vaus, 134)

Slide 7
Frequency Distributions
Ungrouped frequency distribution
A list of each of the values of the variable
The number of times and/or the percent of times each value occurs
Grouped frequency distribution
A table or graph which shows the frequencies or percent for ranges of values
Slide 8
Frequency distributions

Slide 9
Frequency distributions
Required information for frequency tables
table number and title
labels for the categories of the variables
column headings
the number of missing cases
Slide 10
Histograms

Slide 11
Describing Frequency Distributions
Shape
Symmetrical (Mirror image)
Skewed
|
|
Negative skew |
tail toward lower scores
Positive skew
tail toward higher scores
Dispersion
Central tendency
Slide 12
Shape - for ordinal or interval variables

Slide 13
Shape - for ordinal or interval variables

Slide 14
Shape – Symmetry

Slide 15
Central Tendency
Typical or representative value or score
Mean (arithmetic mean)( x )
Sum all the observations / n
Use for interval variables when appropriate
Median
Value that divides the distribution so that an equal number of values are above the median and an equal number below
Mode
Value with the greatest frequency Uni-modal, bi-modal etc.
Slide 16
Mode
Best for nominal variables
Problems
most common may not measure typicality
may be more than one mode
unstable - can be manipulated
Dispersion
variation ratio (v)
% of people not in the modal category
Slide 17
Median
Preferred for ordinal variables
people are ranked from low to high
median is the middle case
the median category is the one that the middle person belongs to

Slide 18
Dispersion
The cth percentile of a set of numbers is a value such that c percent of the numbers fall below it and the rest fall above.
The median is the 50th percentile
The lower quartile is the 25th percentile
The upper quartile is the 75th percentile
five number summary
Median, quartiles and extremes
Slide 19
Dispersion

Slide 20
Boxplot
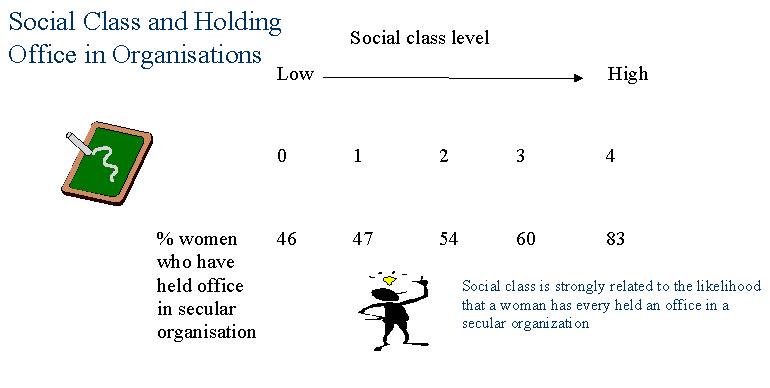
Slide 21
Mean
uses the actual numerical values of the observations
most common measure of centre
makes sense only of interval or ratio data,
frequently computed for ordinal variables as well.
Slide 22
Dispersion
The standard deviation and variance measure spread about the mean as centre.
Variance
mean of the squares of the deviations of the observations from the mean.
Standard deviation
the positive square root of the variance
Slide 23
Example Data (6,7,5,3,4)
Variance (S2)
Calculate the mean for the variable
Take each observation and subtract the mean from it
Square the result from the above
Add (sum) all the individual results
Divide by n
Slide 24
Variance (s2)

Slide 25
Standard deviation (s)
Square root of the variance Ö2 = 1.4
an average deviation of the observations from their mean
influenced by outliers
best used with symmetrical distributions
Slide 26
Summary
Determine if variable is nominal, ordinal or interval
Nominal
Frequency tables
Mode
Ordinal
Frequency tables (grouped frequency tables
histogram
Median and five number summary plus IQR
Mode
Slide 27
Summary
Interval
Determine whether the distribution is skewed or symmetrical
Compare median and mean
Use the mean and the standard deviation if the distribution is not markedly skewed
Otherwise use median and five number summary plus IQR
Use the mode in addition if it adds anything.