Lab 9

In this lab we will explore using the SVD to analyze time series

Contents

Exercise 1: Plotting time series

Download the function

generateData(m)

from the course webpage. This function generates an 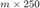$m \times 250$ matrix that represents the evolution of $m$ quantities over the course of 250 days (think stocks, if you're in to that kind of thing, or temperatures if you'd rather think about climate change).

The code

figure(1);
A = generateData(10);
plot(A);
ylim([-10 10]);

will plot the trajectories of the $m$ quantities with a fixed y-axis range.

Exercise 2: Using MATLAB®'s SVD

Next, perform a singular value decomposition of the data
[U,S,V] = svd(A); % A = U*S*V'

Test the decomposition.

Exercise 3: Isolating trajectories

Use the code

figure(1);
A = generateData(10);
plot(A(:,1:2));
ylim([-10 10]);

to plot the time series for the first two quantities. Intuitively, it is clear that if one goes up, the other goes down, but is this a cause and effect relationship? Or is it just coincidental?

Perform

norm(A(:,1) + A(:,2))

to see that one trajectory is not just the negative of the other.

Exercise 4: Showing dependency

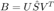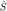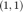Using the SVD, zero out all but the first singular value: Construct a matrix $B = U \hat S V^T$ where $\hat S$ is obtained from $S$ by zero-ing out all entries except the $(1,1)$ entry. Plot the time series $B$:

figure(2);
plot(B);
ylim([-10 10]);

and then consider

norm(B(:,1) + B(:,2))

What do you notice?


Published with MATLAB® R2015a