Lab 8

In this lab we will explore SOR techniques to help iterative methods converge

Exercise 1: Plotting the spectral radius

Given a matrix $A$ , MATLAB® can grab the diagonal, lower-triangular, and upper-triangular parts in a simple way:

A = hilb(5);
D = diag(diag(A));
L = -tril(A,-1);
U = -triu(A,1);

This is the decomposition 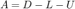$A = D - L - U$ that we use for Jacobi, Gauss-Seidel and SOR. Recall that the matrix in the SOR iteration is

$T_w = (D-wL)^{-1}[(1-w)D + w U].$

Write code to plot the spectral radius of 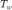$T_w$ as a function of $w$ .

Consider the matrix

A = [2 1 0 0 0; 1 2 1 0 0; 0 1 2 1 0; 0 0 1 2 1; 0 0 0 1 2];
b = ones(5,1);

Find a value of $w$ such that the SOR method converges to a tolerance of 1e-14 in 20 iterations. You can download the SOR code from the website.

Show that the SOR method will never work on the following system:

A = [2 1 1 -1 0; 1 2 1 1 -1; 1 1 2 1 1; -1 1 1 2 1; 0 -1 1 1 2];
b = ones(5,1);