Lab 7
In this lab we will explore relaxation techniques to help iterative methods converge
Contents
Exercise 1: A non-convergent fixed-point method
Consider the fixed-point method given by 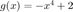 .
.
1) Plot 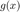 to see that it has a unique fixed point for
to see that it has a unique fixed point for 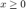 .
.
2) Choose the initial guess  for the fixed point and see that the iteration does not converge.
for the fixed point and see that the iteration does not converge.
3) Consider the associated relaxation method
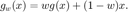
Find a value of  so that this fixed point method converges to a fixed point of
so that this fixed point method converges to a fixed point of 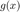 .
.
Exercise 2: Increasing the convergence rate
Consider the fixed-point method given by  . The corresponding fixed-point iteration is (globally) linearly convergent.
. The corresponding fixed-point iteration is (globally) linearly convergent.
1) Find  so that the relaxation method
so that the relaxation method
% 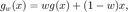 $
$
converges faster to the fixed point of 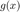 .
.
2) With this choice of  , is the method still globally convergent?
, is the method still globally convergent?
Exercise 3: A non-convergent iterative method
Let
A = [-2 1 0 0 0; 1 -2 1 0 0; 0 1 -2 1 0; 0 0 1 -2 1; 0 0 0 1 -2]; b = [.5, .5, .5, .5, .5]';
Define 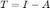 and consider the fixed point method given by
and consider the fixed point method given by 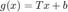 .
.
1) Show that this method does not converge.
2) Consider the associated relaxation method 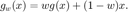 Can you choose
Can you choose  so that the method converges?
so that the method converges?