Lab 6

In this lab we will explore the convergence of iterative methods for linear systems.

Contents

Exercise 1: Simple iteration

Consider

A = [1 .2 .3; -.1 1.1 .3; .2 .5 1];
b = [1 1 1]';

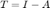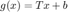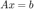Define $T = I-A$ and choose an initial guess $x^{(0)}$. Use the fixed-point iteration function $g(x) = Tx + b$ to solve $Ax = b$. Explain why this fixed-point method converges.

Exercise 2: Less simple iteration

Now consider

A = [1 2.2 0.; -3.1 1.1 0.; 0. 0. .8];
b = [0. 0. 1]';

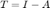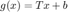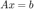Define $T = I-A$ and choose an initial guess $x^{(0)} = [0,0,0]$. Use the fixed-point iteration function $g(x) = Tx + b$ to solve $Ax = b$. Can you explain why this method converges? Try initial guess $x^{(0)} = [1,0,0]$.

Exercise 3: Fixable iteration

Now consider

A = [1 .2 0.; -.3 4 1.; 0. 1. 8];
b = [1 1 1]';

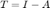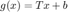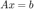Define $T = I-A$ and choose any initial guess $x^{(0)}$. Use the fixed-point iteration function $g(x) = Tx + b$ to solve $Ax = b$. You should observe that this method does not converge. Note that for

D = [1 0 0; 0 4 0; 0 0 8];

We have for 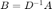$B = D^{-1}A$ where

B = [1/1 .2/1 0./1; -.3/4 4/4 1./4; 0./8 1./8 8/8];

Now change 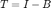$T = I - B$ and use a fixed point iteration 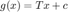$g(x) = Tx + c$ where

c = [1/1 1/4 1/8]';

Compare the answer you get from this fixed point method to

A\b


Published with MATLAB® R2015a