Lab 5

We will consider implmenting the Gauss-Jordan method for computing the inverse of a matrix. In lecture, we discussed that an LU factorization is preferable to compute. But this is instructive as a coding exercise.

Contents

Exercise 1: Gaussian Elimination

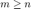Modify your Gaussian elimination w/partial pivoting code (if neccessary) so that it will work an an arbitrary $n \times m$ matrix with $m \geq n$ that is of full rank. Make sure the following code runs:

n = 10;
A = gallery('clement',n,1);
I = eye(n);
GEpp([A,I])

It should return a matrix of the form [U,M] where U is upper-triangular

Exercise 2: Using the last row

Copy your

GEpp(A)

function to a new function

GJtest(A)

Now modify this function so that by using elementary row operations, it returns a matrix of the form [U,M] where the last column of U has only a one in its last entry --- the last column of U is the same as the last column of the identity matrix. Apply it to the same matrix as above.

Exercise 3: Using all the rows

Copy your

GJtest(A)

function to a new function

GJ(A)

Now modify this function so that it returns a matrix of the form [I,M] where I is the identity matrix using only elementary row operations. Apply this to the same matrix as Exercise 1.

Exercise 4: DFT matrix

The discrete Fourier transform (DFT) is a transform that is often used in signal processing and numerical analysis. MATLAB® has it implemented as

fft(v)

for a vector v. The DFT is a linear transformation. Construct its $n \times n$ matrix representation $F$. Notice that it has complex entries. Compute

F*F'

What do you notice?

Exercise 5: Fourier coefficients

Now consider the DFT of a complex exponential sampled on a uniform grid. Change 1j to 2j to -1j to -2j to 0. What do you notice?

n = 10;
x = linspace(0,2*pi,n+1);x = x(1:end-1);
fft(exp(0j*x))/n

For a function 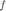$f$ assume

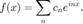
$$f(x) = \sum_{n} c_n e^{i n x}.$$

Can you find a matrix T such that

T*f(x)

gives you the coefficients 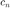$c_n$ (or at least, their approximation)?

Test your code with

$$f(x) = \sum_{i=-\infty}^\infty \frac{e^{i n x}}{|n|!}.$$

Note: you may have to increase 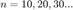$n = 10,20,30...$ to see something...


Published with MATLAB® R2015a