Lab 4

We will consider forward substitution and an iteration scheme for linear systems.

Contents

Exercise 1: Forward substitution

Let $L$ be an $n\times n$ lower triangular matrix with non-zero diagonal entries. We want to solve

$$ Lx = b.$$

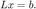
More explicitly:

$$\left[\begin{array}{cccccccc} l_{11} & 0 & 0 &0 & \cdots & 0 \\ l_{21} & l_{22} & 0 & 0 & \cdots & 0 \\ l_{31} & l_{32} & l_{33} & 0 & \cdots & 0 \\ \vdots & &&&& \vdots \\ l_{n1} & l_{n2} & \cdots && \cdots & l_{nn}\end{array}\right] \left[ \begin{array}{c} x_1 \\ x_2 \\ \vdots \\ \vdots \\ x_n \end{array} \right] = \left[ \begin{array}{c} b_1 \\ b_2 \\ \vdots \\ \vdots \\ b_n \end{array} \right].$$

This gives the set of equations

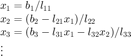
$$ \begin{array}{l} x_1 = b_1/l_{11}\\ x_2 = (b_2 - l_{21} x_1)/l_{22}\\ x_3 = (b_3 - l_{31} x_1 - l_{32} x_2)/l_{33}\\ \vdots \end{array} $$

And in general

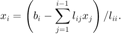
$$ x_i = \left( b_i - \sum_{j=1}^{i-1} l_{ij} x_j \right)/l_{ii}. $$

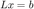Given an augmented matrix, $[L,b]$ implement the forward substitution algorithm to solve $Lx = b$, call your function

Forsub()

Test your algorithm on a matrix $L$ given by

n = 10;
L = rand(n); b = rand(n,1);
for i = 1:n
  for j = i+1:n
     L(i,j) = 0;
  end
end

Exercise 2: An iterative solution

Define matrix 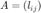$A = (l_{ij})$ for any dimension $n$ by

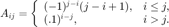
$$A_{ij} = \left\{\begin{array}{lr} (-1)^{j-i} (j-i + 1), & i \leq j,\\ (.1)^{i-j}, & i > j. \end{array}\right.$$

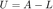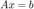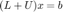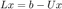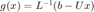Define $L$ to be the lower-triangular part of $A$, and $U = A-L$. If you want to solve $Ax =b$ you can consider $(L + U)x = b$, $Lx = b - Ux$. The solution $x$ is a fixed point of $g(x) = L^{-1}(b-Ux)$.

Use your forward substitution algorithm (and not compute the inverse of L!) and fixed-point iteration to solve for $x$ when $b$ is a vector of all ones. Examine the convergence of the method using

max(abs(x-y))

which returns the maximum entry (in absolute value) of the difference 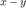$x-y$.


Published with MATLAB® R2015a