Lab 1

This lab will be mostly focused on using for loops and placeholders to implement efficient algorithms. While we are not going to place huge focus on the efficiency of the algorithms we write, we are going to make sure we understand the basics.

Contents

Evaluating Taylor polynomials

Consider the Taylor series expansion for 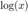$\log(x)$ about $x = 1$:

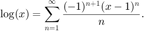
$$\log(x) = \sum_{n=1}^\infty \frac{(-1)^{n+1} (x-1)^{n}}{n}. $$

The partial sums are given by

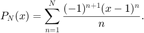
$$P_N(x) = \sum_{n=1}^N \frac{(-1)^{n+1} (x-1)^{n}}{n}. $$

Here is some example code that is not efficient to compute 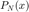$P_N(x)$

%  % Algorithm 1
%  N = 1000;
%  SUM = 0;
%  x = 1.1;
%  for n = 1:N
%      SUM = SUM + (-1)^(i+1)/i*(x-1)^i;
%  end

% We analyze the performance of the algorithm, in part, by using the following
% tic/toc command:

tic
N = 1000;
SUM = 0;
x = 1.1;
for n = 1:N
  SUM = SUM + (-1)^(n+1)/n*(x-1)^n;
end
toc

Elapsed time is 0.001571 seconds.

Exercise 1

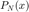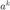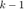First, write an algorithm by modifying the above algorithm for $P_N(x)$, that counts the total number operations (multipications and additions). For simplicity consider $a^k$ as $k-1$ multiplications.

Exercise 2

Using the algorithm written in Example 1 on page 33 of the text (ignoring the error estimate), write an algorithm to compute 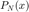$P_N(x)$ than needs only 4N operations to compute N terms. Call this Algorithm 2. Here is the pseudo-code. Make sure you understand why this completes the same task as Algorithm 1.

STEP 1:
  set n = 1; y = x-1; SUM = 0; POWER = y; TERM = y; SIGN = -1;
STEP 2:
  While n <= N do STEPS 3 & 4
STEP 3:
  Set SIGN = - SIGN; SUM = SUM + SIGN*TERM;
     POWER = POWER*y; TERM = POWER/(n+1);
STEP 4:
  Set n = n+1;
STEP 5:
  OUTPUT(SUM);

Exercise 3

Using the break command

break;

perform the following. Assume you only have limited resources and can only use 1000 operations. Approximate 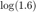$\log (1.6)$ using Algorithms 1 & 2, counting your operations as you go, and breaking out of the for loop when 1000 operations have been counted. What is the error for each algorithm? How many terms did you compute?


Published with MATLAB® R2015a