Lab 0

Contents

Preliminaries

The lab section of this course gives an opportunity to implement the ideas that come from lecture. Numerical analysis allows one to experiment directly with ideas from calculus, linear algebra and beyond.

The grade for this lab section is based on weekly homework assignments assigned in lecture (50%) and a final project (50%). Not all homework assignments will have a lab assignment.

Homework is due at the end of the day the Thursday after it is assigned. We will take lab time to work on the assignments. Late assignments will not be accepted.

The project will assigned early in the quarter and will be due at the end of the day on Dec. 8. It will consist of an in-depth coding project.

In this class we will use the "publish" functionality of MATLAB® extensively. All MATLAB work that is turned it should be written so that it is readable after "publishing it". Please see me or the TA if you have any questions about this functionality. Here is the official documentation for publishing: Publishing Markup

MATLAB® Links

UCI MATLAB Software Installation

Some other references for MATLAB® tutorials are:

MATLAB primer

Additional MATLAB tutorials

Another MATLAB tutorial

Some basic commands

clear % clear workspace
1 + 1
sin(pi*3)
exp(-1)
tanh(20)

ans =

     2


ans =

   3.6739e-16


ans =

    0.3679


ans =

     1

Defining vectors

v = [1 2 3]; % a row vector, semi-colon supresses output
w = [1; 2; 3]; % a column vector
v - w' %' gives the transpose

ans =

     0     0     0

Long vectors

v = [1:9] % a vector of integers 1 through 9
v(1) % first element of v
v(end) % last element of v
v(2:7) % grab elements 2 through 7
v(4:end) % grab elements 4 through the end

v =

     1     2     3     4     5     6     7     8     9


ans =

     1


ans =

     9


ans =

     2     3     4     5     6     7


ans =

     4     5     6     7     8     9

Matrices

M = [1,2,3,4;5,6,7,8;9,10,11,12;12,14,15,16]
M(1,4) % get the (1,4) element
M(2:3,2:3) % get the "middle" block of the matrix

M =

     1     2     3     4
     5     6     7     8
     9    10    11    12
    12    14    15    16


ans =

     4


ans =

     6     7
    10    11

Plotting

x = linspace(-1,1,100); % use 100 points between -1 and 1;
y = sin(x);
figure(1) % select a figure
plot(x,y)

x = -1:.1:1; % points from -1 to 1 with a spacing of .1;
y = x.^2; % use .^ or .* or ./ apply this operations to vectors componentwise
figure(2)
plot(x,y)

Plotting two functions with labels

x = linspace(-1,1,100);
figure(3)
plot(x,sin(x),'r') % plot in red
hold on % prevent the figure from being overwitten
plot(x,x.^2,'k') % plot in black
xlabel('x')
ylabel('y')

for loops (notice the tab's for text alignment)

The following should give the sum of the first 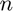$n$ integers which is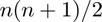 $n(n+1)/2$

n = 10;
SUM = 0; % using capital letters because sum() is a built-in function
for i = 1:n
    SUM = SUM + i;
end
SUM
n*(n+1)/2

SUM =

    55


ans =

    55

a function

We can define anonymous functions in this way:

g = @(n) sum([0:n]);
g(10)

ans =

    55

Problem 1:

Define

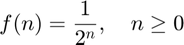
$$ f(n) = \frac{1}{2^n}, \quad n \geq 0$$

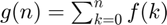Write code to plot the two functions $f(n)$ and $g(n) = \sum_{k=0}^n f(k)$ for $0 \leq n \leq 20$. The command

plot(x,y,'*')

will plot the function but not interpolate between data points. Hint: look at the

cumsum()

command.

Problem 2:

Define the matrix

$$ M = \left[ \begin{array}{ccc} 1 & 2 & 1 \\ 2 & 4 & 3 \end{array} \right].$$

Write code to subtract twice the first row from the second.


Published with MATLAB® R2016a