Homework 7

Section 7.4: 7, 9

Section 9.2: 1b, 3a, 6a, 12, 14

Computer Assignment 7
Part 1:
Part 2:
Solution

Computer Assignment 7

Due Thursday, Nov 17 at 11:59pm

Part 1:

Implement the Jacobi algorithm to solve 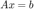$A x = b$ .

INPUT: An n x n matrix A, a right-hand side b, an initial guess x0, tolerance TOL and maximum number
of iterations Nmax

OUTPUT: An approximate solution x or a message of failure

STEP 1: set x = x0;
STEP 2: For k = 1,2,...,Nmax do STEPS 3-7
  STEP 3: Set xold = x;
  STEP 4: For i =1,2,...,n do STEPS
    STEP 5: Set SUM = -sum( A(i,j)*xold(j), i ~= j) + b(i)
    STEP 6: Set x(i) = SUM/A(i,i)
  STEP 7: If max(abs(x-xold)) < TOL
    PRINT('Solution found in  %d iterations', k)
    RETURN(x)
    STOP.
STEP 8:
  PRINT('Maximum number of iterations reached, Nmax = %d',Nmax)
  RETURN(x)
  STOP.

Apply this algorithm to the linear system

A = [10,1,-1,3; 2, 11, 4, 0; -3, 1, 9, 4; 1, 1, 1, 10];
b = [1,-1,1,-1]';

with

TOL = 1e-12;

How many iterations are required to acheive this tolerance for the follow two initial guesses?

x0 = [0,0,0,0]';
x0 = [.18,-.22,.25,-.12];

Explain why the second initial guess gives fewer iterations.

Part 2:

Implement the Gauss-Seidel algorithm to solve 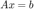$A x = b$ .

INPUT: An n x n matrix A, a right-hand side b, an initial guess x0, tolerance TOL and maximum number
of iterations Nmax

OUTPUT: An approximate solution x or a message of failure

STEP 1: set x = x0;
STEP 2: For k = 1,2,...,Nmax do STEPS 3-7
  STEP 3: Set xold = x;
  STEP 4: For i =1,2,...,n do STEPS
    STEP 5: Set SUM = -sum( A(i,j)*x(j), j=1,2,...,i-1) - sum( A(i,j)*xold(j), j=i+1,i+2,...,n) + b(i)
    STEP 6: Set x(i) = SUM/A(i,i)
  STEP 7: If max(abs(x-xold)) < TOL
    PRINT('Solution found in  %d iterations', k)
    RETURN(x)
    STOP.
STEP 8:
  PRINT('Maximum number of iterations reached, Nmax = %d',Nmax)
  RETURN(x)
  STOP.

Again, apply this algorithm to the linear system

A = [10,1,-1,3; 2, 11, 4, 0; -3, 1, 9, 4; 1, 1, 1, 10];
b = [1,-1,1,-1]';