Homework 5

Section 6.3: 1d, 2c, 5b, 9c, 11b

Section 6.4: 1b, 6, 8, 10

Section 6.5: 4a, 5a, 6a

Computer Assignment 5
Solution

Computer Assignment 5

Due Thursday, Nov 3 at 11:59pm

Use the pseudocode given below to implement a function GEcp() that performs Gaussian elimination with complete pivoting. This is very involved so it is suggested that you look at this early.

function [A,X] = GEcp(A)

INPUT: A is an n x m matrix

OUTPUT:  A an n x m upper-triangular matrix and a vector X that tracks the reordering of the unknowns, or a message of failure

STEP 1: Set X = [1,2,3,...,n]^T;
STEP 2: For i = 1,2,...,n-1 do STEPS 3-10
  STEP 3: Set MAX to be the maximum of max(abs(A(j,i:n)) for j =
  i,i+1,..,n
  STEP 4: If MAX = 0 then
    DISPLAY('Method failed: matrix is rank deficient')
    OUTPUT(A);
    STOP.
  STEP 5: Let p be the smallest number such that MAX = max(abs(A(p,i:n));
  STEP 6: Let q be the smallest number such that MAX = max(abs(A(p,q)));
  STEP 7: Do Ri <--> Rp on A;
  STEP 8: Do Ci <--> Cq on A;
  STEP 9: Do Ri <--> Rq on X;
  STEP 10: For j = i+1,i+2,...,n do STEP 6
    STEP 11: Do Rj - A(j,i)/A(i,i) Ri --> Rj on A
STEP 12: OUTPUT([A,X]); STOP.

The output of this function when called by

[U,X] = GEcp([A,b])

is an upper triangular 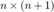$n \times (n+1)$ matrix U and a vector X that tracks the unknowns after column operations. You can then solve for the permuted unknowns with

y = Backsub(U);

Then you must reverse the swaps via:

x = zeros(n,1);
for i = 1:n
     x(X(i)) = y(i);
end

First confirm that your code works. Then perform the following test (This requires your GE and Backsub code. You may use the solution code, if you like.):

n = 60;
errorGE = zeros(100,1); errorGEcp = zeros(100,1);
for j = 1:100
  A = rand(n);  b = rand(n,1);
  A(1,:) = A(2,:) + 0.000001*A(1,:);

  errorGE(j) = max(abs(A*Backsub(GE([A,b]))-b));

  [U,X] = GEcp([A,b]);
  y = Backsub(U);
  x = zeros(n,1);
  for i = 1:n
     x(X(i)) = y(i);
  end
  errorGEcp(j) = max(abs((A*x-b));
end
mean(errorGEcp)
mean(errorGE)

Comment on what this test doing and what you notice about the output.

Solution

function [A,X] = GEcp(A)
   % your function here
end

Homework 5

Contents

Computer Assignment 5

Solution