Homework 4

Section 6.1: 5a, 6a, 9, 12

Section 6.2: 1b, 5b, 31

Contents

Computer Assignment 4

Due Thursday, Oct 20 at 11:59pm

Use the pseudocode given below to implement both a Gaussian elimination function GE() and a backward substitution function Backsub().

function A = GE(A)
INPUT: A is an n x m matrix
OUTPUT:  A an n x m upper-triangular matrix, or Inf if the method failed
STEP 1: For i = 1,2,...,n-1 do STEPS 2-5
STEP 2: Let p >= i be the smallest integer such that A(p,i) ~= 0.
STEP 3: If p cannot be found then
  DISPLAY('Method failed: matrix is rank deficient')
  OUTPUT(A);
  STOP.
STEP 4: If p > i do Ri <--> Rp on A
STEP 5: For j = i+1,i+2,...,n do STEP 6
  STEP 6: Do R_j - A(j,i)/A(i,i) R_i --> R_j on A
STEP 7: If A(n,n) = 0
  DISPLAY('Method failed: matrix is rank deficient')
  OUTPUT(A)
STEP 8: OUTPUT(A); STOP.
function x = Backsub(U)
INPUT: U is an n x n + 1 upper-triangular matrix with non-zero diagonal entries
OUTPUT: the solution to U(1:n,1:n)x=U(1:n,n+1)
STEP 1: Set x = U(:,n+1);
STEP 2:
  If U(n,n) = 0 then
      OUTPUT('Method failed: singular matrix')
      STOP.
  Else set x(n) = U(n,n+1)/U(n,n);
STEP 3: For i = n-1,...,1 do STEP 4
  STEP 4:
    If U(i,i) = 0 then
      OUTPUT('Method failed: singular matrix')
      STOP.
    Else set
      x(i) = U(i,n+1) - SUM( U(i,j)x(j), j= i+1,...,n );
      x(i) = x(i)/U(i,i).
STEP 5: OUTPUT(x); STOP.

NOTE: In the Backsub() pseudo-code the function SUM( U(i,j)x(j), j= i+1,...,n ) is equivalent to

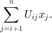
$$ \sum_{j = i +1}^n U_{ij} x_j. $$

(1) You should demonstrate that your code works to solve 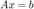$A x = b$ when $A$ is invertible (i.e. non-singular) and gives an error message when $A$ is singular. Test your code on different-dimensional linear systems. Using the

rand()

command will help you generate matrices of varying sizes.

(2) Consider the $n \times n$ upper-triangular matrix defined by

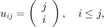
$$u_{ij} = \left(\begin{array}{cc} j \\ i \end{array}\right), \quad i \leq j,$$

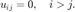
$$ u_{ij} = 0, \quad i > j.$$

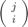Here $\left(\begin{array}{cc} j \\ i \end{array}\right)$ is the binomial coefficient

binomial(j,i)
binomial = @(j,i) factorial(j)/(factorial(i)*factorial(j-i));

If $U$ is defined in this way, then the following code constructs the inverse matrix 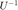$U^{-1}$:

Uinv = eye(n);
for i = 1:n
     Uinv(:,i) = Backsub([U,Uinv(:,i)]);
end

Implement this and show that you do indeed compute the inverse.

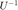EXTRA CREDIT: Make a guess as to what the $(i,j)$ entry of $U^{-1}$ is (the total for the assignment can't exceed 10pts)

Solution

function A = GE(A)
    % your function here
end


function x = Backsub(U)
   % your function here
end


Published with MATLAB® R2015a