Homework 3

Section 2.4: 7a, 10, 13

Section 2.5: 1d, 17

Contents

Computer Assignment 3

Due Thursday, Oct 13 at 11:59pm

Write a function hornerroots(a,p0,TOL,Nmax) that performs a Newton iteration, using Horner's method to evaluate the polynomial and its derivative, to compute the zeros of the polynomial with coefficients a = [a(1) a(2) a(3) ... ]. Define

n = length(a)

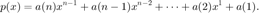
$$p(x) = a(n) x^{n-1} + a(n-1) x^{n-2} + \cdots + a(2) x^1 + a(1).$$

Note that

a(1)

is the same as $a_0$, for example. Here is the pseudocode

INPUT: coefficients a, an initial guess p0, tolerance TOL, maximum number of
iterations Nmax
OUTPUT: an approximate root p found with Newton's method
STEP 1: Set p = p0; Set n = length(a)
STEP 2: For j = 1,2,...,Nmax do STEPS 3-10
  STEP 3: Set b = a(n)
  STEP 4: Set c = a(n)
  STEP 5: Set i = n
  STEP 6: While i > 2
    SUBSTEP 1: Set i = i - 1
    SUBSTEP 2: Set b = a(i) + b*p
    SUBSTEP 3: Set c = b + c*p
  STEP 7:  Set b = a(1) + b*p
  STEP 8: Set pold = p
  STEP 9: Set p = p - b/c;
  STEP 10: If |p-pold| < TOL
        OUTPUT(p)
        STOP.
STEP 11: OUTPUT('Method failed after Nmax iterations Nmax =', Nmax)

Then use your function to compute ALL 10 roots of of the polynomial where

a = [-63 0 3465 0 -30030 0 90090 0 -109395 0 46189]/256;

You will need to run your Newton iteration with the initial guesses:

n = (2*[1:10]-1)/20*pi;
approxroots = cos(n);

Solution

Write your solution here


Published with MATLAB® R2015a