Homework 2

Section 2.2: 3, 7, 11a, 18, 21

Section 2.3: 1, 3a, 15, 19

Computer Assignment 2
Solution

Computer Assignment 2

Due Thursday, Oct 6 at 11:59pm

In lab this week, we discussed the construction of MATLAB® functions. In versions of MATLAB® before R2016a, functions cannot be defined in a script. They have to be defined in a separate file. For that reason, I will stick with this convention, but you need not.

Part 1

Create a function fixedpoint(g,p0,TOL,Nmax) that performs the following

INPUT: a function g, initial guess p0, error tolerance TOL and maximum
number of interations Nmax

OUTPUT:  An approximate fixed point p, or message of failure

STEP 1: Set pold = p0;  p = g(pold);
STEP 2: For i <= Nmax do STEPS 3-4
  STEP 3: If |p-pold| < TOL
    OUTPUT(p);
    STOP.
  STEP 4: Set pold = p; p = g(p);
STEP 5: OUPUT('The method failed after Nmax iterations, Nmax = ', Nmax);
  STOP;

Use your function to approximate 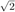$\sqrt{2}$ by using 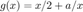$g(x) = x/2 + a/x$ and choosing $a$ appropriately. Demonstrate that increasing the tolerance gives better accuracy. Explain your output.

Part 2

Create a function newton(f,df,p0,TOL,Nmax) that performs the following

INPUT: a function f and its derivative df, initial guess p0, error tolerance TOL and maximum
number of interations Nmax

OUTPUT:  An approximate root of f using Newton's method

STEP 1: Set pold = p0;
STEP 2: p = p0 - f(p0)/df(p0);
STEP 3: For i <= Nmax do STEPS 4-5
  STEP 4: If |p-pold| < TOL
    OUTPUT(p);
    STOP.
  STEP 5: Set pold = p; p - f(p)/df(p);
STEP 6: OUPUT('The method failed after Nmax iterations, Nmax = ', Nmax);
  STOP;

Use your function to solve Problem 23 in Section 2.2.

Solution

Put your name and solution here.

Part 1 Solution

function p = fixedpoint(f,p0,TOL,Nmax)
 %write your function here

end

Part 2 Solution

function p = newton(f,df,p0,TOL,Nmax)
 %write your function here

end