Homework 1

Section 1.2: 2c, 3d, 12

Show that the nesting algorithm for computing 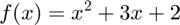$\displaystyle f(x) = x^2 + 3x + 2$ reduces roundoff error in 3-digit machine arithmetic.

Section 2.1: 3a, 5b, 11c, 14

Contents

Computer Assignment 1

Complete the following assignment and turn it in to the eee.uci.edu DropBox by 11:59pm, Tuesday, 10/4. You should use MATLAB's publish functionality and submit both a .pdf file and your original m-file. If you have any questions about this, please ask. You should just modify this file when you submit.

Implement the bisection method (Algorithm 2.1 on pg. 49) and use it to compute the root of

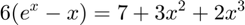
$$6(e^x - x) = 7 + 3 x^2 + 2 x^3$$

that lies in the interval $[-1,1]$.

INPUT endpoints a,b; tolerance TOL; maximum number of iterations Nmax
OUTPUT approximate solution x of f(x) = 0; or failure message
Step 1: Set i = 1;
      A = f(a);
Step 2:  While i <= Nmax do 3-6:
     Step 3: Set p = (a+b)/2; P = f(p);
     Step 4: If P = 0 or (b-a)/2 < TOL then
     Step 5: OUTPUT(p);
             STOP.
     Step 6: If A*P > 0 then set a = p; A = P;
                 Else set b = p;
Step 7: OUPUT('Method failed after Nmax iterations, Nmax = ', Nmax);
        STOP.

Solution

Put your name and solution here.


Published with MATLAB® R2015a