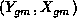 are available in
are available in  groups with at most
groups with at most 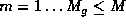 in each group, and that the mean and variance of each observation is thought to satisfy a generalised linear model:
in each group, and that the mean and variance of each observation is thought to satisfy a generalised linear model:
Suppose observations and p covariates 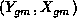 are available in
are available in  groups with at most
groups with at most 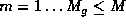 in each group, and that the mean and variance of each observation is thought to satisfy a generalised linear model:
in each group, and that the mean and variance of each observation is thought to satisfy a generalised linear model:

but that the observations within a group are correlated. If the variables were uncorrelated the (quasi)score equations would be:
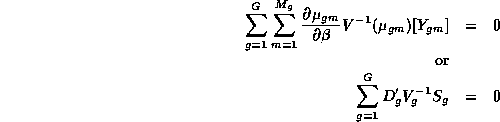
where 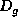 is
is 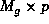 matrix of derivatives,
matrix of derivatives, 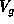 is a diagonal
is a diagonal 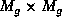 matrix of variances and
matrix of variances and 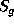 is the vector of the
is the vector of the 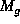 residuals
residuals 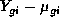 .
.
The left-hand side of this equation has zero expectation at the true value of  even if there is correlation within groups, so the estimates of
even if there is correlation within groups, so the estimates of  will be consistent even for correlated data. In this equation the changing variance of
will be consistent even for correlated data. In this equation the changing variance of 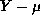 is accounted for in the weighting by
is accounted for in the weighting by  but no account is made for the correlations. The consistency results still hold if
but no account is made for the correlations. The consistency results still hold if  is replaced by a covariance matrix for group g, either prespecified or depending on a finite set of parameters. If this covariance matrix is close to the true covariance of
is replaced by a covariance matrix for group g, either prespecified or depending on a finite set of parameters. If this covariance matrix is close to the true covariance of  then
then 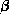 will be estimated more efficiently. The assumed form of
will be estimated more efficiently. The assumed form of 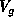 is called the ``working covariance model''.
is called the ``working covariance model''.
In order for this to be useful it is necessary to have reliable standard error estimates for the estimates 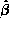 . An argument based on the delta method (or a first-order Taylor series expansion) shows that
. An argument based on the delta method (or a first-order Taylor series expansion) shows that
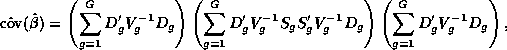
the so-called ``sandwich estimator'' gives asymptotically correct standard errors and various simulation studies have shown that its properties are good when M is small (5 or fewer). Less is known for large M.