


Next: Options controlled by
Up: Theoretical and Computational
Previous: Extending the software
The saturated correlation model estimates all the pairwise correlation parameters separately. There is a unique sensible estimate of the covariance matrix (assuming a balanced design) but not of the correlation matrix. The problem is that the diagonal elements of the covariance matrix are assumed equal under the model but will not be estimated as equal. The method used in the S gee() library, the Stata xtgeecommand and Karim & Zeger's GEE macro for SAS is to estimate the dispersion 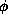 by the variance of the Pearson residuals, to estimate the correlations
by the variance of the Pearson residuals, to estimate the correlations  by
by
 for
for  where
where  are the set of Pearson residuals at time i and to set
are the set of Pearson residuals at time i and to set 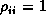 . The Biometrika paper used a similar estimate but did not set the diagonals to 1. This gives the ML estimate of the covariance matrix if the dispersion is not assumed constant over time. A third possibility would be to use the Normal ML estimate of the correlation matrix. It is not clear which is best, but most of the programs have settled on the same choice to make software testing easier. There is one significant disadvantage of this choice: it is the only one where the ``correlation matrix'' need not be positive definite. This can happen when the sample size is not large relative to the number of correlations being estimated and especially if the true time-specific variances are not all the same. It can only happen for three or more time points as for two time points the arithmetic-geometric mean inequality guarantees that the estimated correlation will be less than the usual estimate. The usual choice (diagonals forced to 1) is correlation structure saturated-corr, the covariance matrix divided by the scale parameter (Zeger & Liang's estimate, and the one given in the book by Fahrmeir & Tutz) is saturated-ml-corr
. The Biometrika paper used a similar estimate but did not set the diagonals to 1. This gives the ML estimate of the covariance matrix if the dispersion is not assumed constant over time. A third possibility would be to use the Normal ML estimate of the correlation matrix. It is not clear which is best, but most of the programs have settled on the same choice to make software testing easier. There is one significant disadvantage of this choice: it is the only one where the ``correlation matrix'' need not be positive definite. This can happen when the sample size is not large relative to the number of correlations being estimated and especially if the true time-specific variances are not all the same. It can only happen for three or more time points as for two time points the arithmetic-geometric mean inequality guarantees that the estimated correlation will be less than the usual estimate. The usual choice (diagonals forced to 1) is correlation structure saturated-corr, the covariance matrix divided by the scale parameter (Zeger & Liang's estimate, and the one given in the book by Fahrmeir & Tutz) is saturated-ml-corr



Next: Options controlled by
Up: Theoretical and Computational
Previous: Extending the software
Thomas Lumley
Sun Dec 8 16:10:41 PST 1996
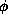 by the variance of the Pearson residuals, to estimate the correlations
by the variance of the Pearson residuals, to estimate the correlations  by
by
 for
for  where
where  are the set of Pearson residuals at time i and to set
are the set of Pearson residuals at time i and to set 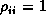 . The Biometrika paper used a similar estimate but did not set the diagonals to 1. This gives the ML estimate of the covariance matrix if the dispersion is not assumed constant over time. A third possibility would be to use the Normal ML estimate of the correlation matrix. It is not clear which is best, but most of the programs have settled on the same choice to make software testing easier. There is one significant disadvantage of this choice: it is the only one where the ``correlation matrix'' need not be positive definite. This can happen when the sample size is not large relative to the number of correlations being estimated and especially if the true time-specific variances are not all the same. It can only happen for three or more time points as for two time points the arithmetic-geometric mean inequality guarantees that the estimated correlation will be less than the usual estimate. The usual choice (diagonals forced to 1) is correlation structure saturated-corr, the covariance matrix divided by the scale parameter (Zeger & Liang's estimate, and the one given in the book by Fahrmeir & Tutz) is saturated-ml-corr
. The Biometrika paper used a similar estimate but did not set the diagonals to 1. This gives the ML estimate of the covariance matrix if the dispersion is not assumed constant over time. A third possibility would be to use the Normal ML estimate of the correlation matrix. It is not clear which is best, but most of the programs have settled on the same choice to make software testing easier. There is one significant disadvantage of this choice: it is the only one where the ``correlation matrix'' need not be positive definite. This can happen when the sample size is not large relative to the number of correlations being estimated and especially if the true time-specific variances are not all the same. It can only happen for three or more time points as for two time points the arithmetic-geometric mean inequality guarantees that the estimated correlation will be less than the usual estimate. The usual choice (diagonals forced to 1) is correlation structure saturated-corr, the covariance matrix divided by the scale parameter (Zeger & Liang's estimate, and the one given in the book by Fahrmeir & Tutz) is saturated-ml-corr