


Next: Extending the software
Up: Theoretical and Computational
Previous: Performance
One feature of GEEs and the generalised linear models from which they arose is the ability to combine arbitrary link and variance functions. Some care is needed to ensure that the numerical estimation doesn't crash when strange combinations of link and variance are chosen. The :compute-step-beta method contains a check that the new values of the regression coefficient produce valid values for the linear predictor and the fitted mean. If this is not the case then the step size is halved and the check repeated until the values are valid. A warning message is also printed.
If there is no solution to the estimating equations in the permissible parameter space (as might happen with binomial error and identity link, for example), the algorithm will converge to a point on the boundary of the parameter space which will be a local extremum of the estimating function. The corresponds to finding the maximum of a likelihood at the boundary of the parameter space. There is one situation when the program may crash rather than producing a solution, when the data are inconsistent with the chosen error function. The only example likely to occur is trying to fit the Gamma error model to data with observed zeroes.
The choice of starting values for the regression parameters is also complicated when the link and variance can be chosen arbitrarily (this is a disadvantage of not using iterated reweighted least squares). The program deals with three cases. For all the commonest models  gives valid estimates. For models where this is not the case (eg gamma/reciprocal link, power variance/power link) the initial values depend on whether the model contains an intercept. If it does then all the other regression parameters are set to 0 and the intercept is chosen to give valid starting values. If there is no intercept then a valid set of starting values need not exist. The program tries
gives valid estimates. For models where this is not the case (eg gamma/reciprocal link, power variance/power link) the initial values depend on whether the model contains an intercept. If it does then all the other regression parameters are set to 0 and the intercept is chosen to give valid starting values. If there is no intercept then a valid set of starting values need not exist. The program tries 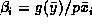 (where
(where 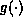 is the link function) and if this doesn't work it gives up and asks for starting values to be specified.
is the link function) and if this doesn't work it gives up and asks for starting values to be specified.
In data sets with only a small number of groups it may not be possible to estimate all the parameters in certain correlation structures and the code will crash. If the program will not run with a certain correlation structure then it is probably wise to choose a simpler structure. As mentioned in Section 2, the standard error estimates may be unreliable when the number of groups is not larger, and if the correlation matrix is not well-determined by the data there is no guarantee that the method is even consistent.



Next: Extending the software
Up: Theoretical and Computational
Previous: Performance
Thomas Lumley
Sun Dec 8 16:10:41 PST 1996
 gives valid estimates. For models where this is not the case (eg gamma/reciprocal link, power variance/power link) the initial values depend on whether the model contains an intercept. If it does then all the other regression parameters are set to 0 and the intercept is chosen to give valid starting values. If there is no intercept then a valid set of starting values need not exist. The program tries
gives valid estimates. For models where this is not the case (eg gamma/reciprocal link, power variance/power link) the initial values depend on whether the model contains an intercept. If it does then all the other regression parameters are set to 0 and the intercept is chosen to give valid starting values. If there is no intercept then a valid set of starting values need not exist. The program tries 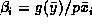 (where
(where 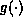 is the link function) and if this doesn't work it gives up and asks for starting values to be specified.
is the link function) and if this doesn't work it gives up and asks for starting values to be specified.