


Next: Performance
Up: Theoretical and Computational
Previous: Theoretical and Computational
The main computations are carried out in the method :compute-step-beta. This does not use the iteratively reweighted least squares method of glim-proto which would require rewriting regression-proto to handle non-diagonal weight matrices (feasible) and would involve inverting 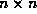 matrices (undesirable). As observations in different groups are independent the weight matrix is block diagonal and so is mostly easily dealt with in blocks correponding to the groups. This only requires inverting the correlation matrix for each group and the final quasi-information matrix, all of which are small. The algorithm is as described by Liang & Zeger (1986), and is similar to Fisher scoring, with iteration continued until either the parameter estimates or the ``independence model deviance'' changes by less than *gee-tolerance*. Variable names in compute-step-beta are generally based on the notation in that paper. Some of the correlation estimates are slightly modified from the original paper to agree with other software.
matrices (undesirable). As observations in different groups are independent the weight matrix is block diagonal and so is mostly easily dealt with in blocks correponding to the groups. This only requires inverting the correlation matrix for each group and the final quasi-information matrix, all of which are small. The algorithm is as described by Liang & Zeger (1986), and is similar to Fisher scoring, with iteration continued until either the parameter estimates or the ``independence model deviance'' changes by less than *gee-tolerance*. Variable names in compute-step-beta are generally based on the notation in that paper. Some of the correlation estimates are slightly modified from the original paper to agree with other software.
The information required for the deletion diagnostics is computed by the same function as updates the regression parameter estimates. At the moment this information is not computed in the usual fitting process and another iteration is required the first time any deletion diagnostics are calculated. It would be possible to calculate this information while the model is fitted. This would cause extra garbage collection but would save time in plotting diagnostics. To do this, set the global variable *gee-diagnostics-while-fitting* to t. Variable names in the deletion diagnostic methods are based on the notation of Preisser & Qaqish, and so differ from those in the rest of the code.
As mentioned above, the functions do not assume that the data are presorted by group and observation time and instead require that observation times are supplied for any correlation structure where it would make a difference. This is because missing data handling is practically impossible without having a record of observation times (a recent version of a SAS macro introduces observation times to handle missing cases). It is also safer: other packages will give you the wrong answer with no warning if the data are not sorted by time within group. The way this is now implemented is not very efficient: asymptotically the calculation time is dominated by the time taken to find each group. More efficient code using hash tables would be possible. In practical examples, though, this is not a real issue. For very large data sets it is clearly worth assuming the data are sorted but it is also worth writing special-purpose compiled code.
As the observations within a group may vary in number and be in random order the correlation structures use an association list to match up the :times variable with the appropriate indices for selecting a submatrix of the correlation matrix. This produces very simple code for the method that returns the inverse correlation matrix and also simplifies the code for estimating correlations.



Next: Performance
Up: Theoretical and Computational
Previous: Theoretical and Computational
Thomas Lumley
Sun Dec 8 16:10:41 PST 1996
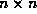 matrices (undesirable). As observations in different groups are independent the weight matrix is block diagonal and so is mostly easily dealt with in blocks correponding to the groups. This only requires inverting the correlation matrix for each group and the final quasi-information matrix, all of which are small. The algorithm is as described by Liang & Zeger (1986), and is similar to Fisher scoring, with iteration continued until either the parameter estimates or the ``independence model deviance'' changes by less than *gee-tolerance*. Variable names in compute-step-beta are generally based on the notation in that paper. Some of the correlation estimates are slightly modified from the original paper to agree with other software.
matrices (undesirable). As observations in different groups are independent the weight matrix is block diagonal and so is mostly easily dealt with in blocks correponding to the groups. This only requires inverting the correlation matrix for each group and the final quasi-information matrix, all of which are small. The algorithm is as described by Liang & Zeger (1986), and is similar to Fisher scoring, with iteration continued until either the parameter estimates or the ``independence model deviance'' changes by less than *gee-tolerance*. Variable names in compute-step-beta are generally based on the notation in that paper. Some of the correlation estimates are slightly modified from the original paper to agree with other software.