
|
Dividing by n - 1
Dividing the sum of squares by (n - 1) instead
of just n is one of the mysteries that
often puzzles students of statistics. It is not something to worry
too much about because with lots of observations it won't matter much
whether you divide by (n - 1) or n.
But the explanation is not that complicated and leads us to the important
statistical concept of degrees of freedom.
Suppose there were five scores--five independent pieces of information.
If asked to guess the scores, you would
have no idea what to guess--the scores could be any value. Now suppose that
you were told that the mean of the five scores equaled 10. Now would you have
any idea what to guess for the five scores. Not really, the scores could still
be almost anything. Finally, suppose that you were also told that four of the
scores were:
Now can you guess the missing fifth score? Yes, we can determine what
the last number must be to make the average of all five numbers be 10.
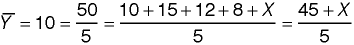
In this case, 45 + X = 50 so the missing score
must equal 5. In other words, once we know the mean, then only n - 1
(four in this case) of the scores are "free to vary." The last score
is not free to vary because it must be exactly what is required to
produce the mean. Once we know the mean, then there are only n - 1
pieces of independent information remaining in the data. Therefore, when
calculating the standard deviation using the mean, the data and hence the
errors and hence the squared errors only contain n - 1
independent pieces of information. The last error and its square are
determined. When calculating the errors for the standard deviation we
thus say that the data have only n - 1 degrees
of freedom. The general rule is that each time we estimate something
from the data, we must subtract one degree of freedom from n.
|

|
|
File:
© 1999, Duxbury Press.
|
|
|