We now have all the parts we need to test hypotheses using Student's t-test. In our example we wanted to know whether these study hour ratios from fifteen students are sufficient evidence to reject the null hypothesis that students study two hours outside class for each hour of classtime:

1.9   2.1   1.2   0.7   1.8   1.6   2.4   3.0   0.9   1.3   1.5   1.9   2.0

Should this null hypothesis be rejected in favor of this alternative hypothesis?

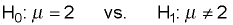
The mean for the study hour ratios is 1.715 and the standard deviation is 0.62. When this page loads, these values are in the graph below, which calculates the t-test value and its two-tailed probability.

The probability of getting a value of the t-test statistic this extreme (i.e., this far away from zero) if the null hypothesis were true is 0.123. Because this is greater than 0.05, the value of the t-test statistic is not surprising enough to reject the null hypothesis that students study two hours outside class for each hour in class.