Relationship between PRE and t

Relationship between PRE and Student's t

There is a close relationship between the value of Student's t-statistic and the value of the proportional reduction in error (PRE).

Sums of Squared Errors

The sum of squared errors when using the null hypothesis is given by

and the sum of squared errors when using the mean, i.e., the best estimate of the alternative hypothesis, is given by

The sum of squares reduced is simply the difference between these two sums of squares. SSE0 is necessarily as least as large as SSE1 so the difference will always be nonnegative. The following algebraic manipulations produce a useful expression for SSR.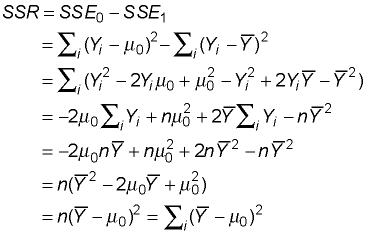

sum of squares reduced and its re-expression

Expressing Student's t in terms of SSE

Now let's consider the square of Student's t, rearrange it slightly and make appropriate substitutions in terms of the sums of squares (including PRE = SSR/SSE0):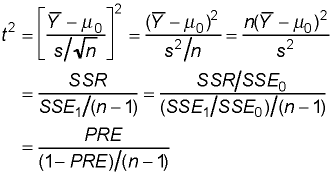

Thus, if we know PRE we can easily calculate the square of Student's t. Then, solving the above for PRE, we find this expression for PRE in terms of the square of Student's t: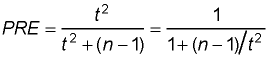

Therefore, if we know the surprise or critical values for Student's t, we can use the above formula to find the corresponding surprise or critical values for PRE. For the example in the text page for which n = 13, df = n - 1 = 12, the 5-percent and 1-percent surprise values for Student's t are 2.18 and 3.05, respectively. Substituting in the previous equation gives the 5-percent surprise value of PRE as

A similar calculation gives the 1! surprise value of PRE as .44. Both these values are indicated as horizontal lines in the error meter.