transpcr.gif (812 bytes) The normal distribution is very useful for telling us how likely are ranges of possible scores. The proportional area under the normal density curve between two scores corresponds to the probability of getting a score in that range. The total area under the curve is of course 100 percent. The mean and the median are the same for the normal distribution, so 50 percent of the scores are equal to or below the mean as depicted in this graph.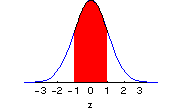

As can be seen in this graph, a large proportion of the observations are likely to occur between z-scores of -1 and +1 (that is, to be within one standard deviation of the mean). Estimate the approximate proportion depicted; later we will calculate it exactly using the interactive graphs below.

Use this graph to calculate z-scores and to see the corresponding probabilities. Any number can be changed, but the change will not be effective until you press the return key while in one of the boxes. You may also change the portion of the normal distribution selected:
 
  • Cumulative--from minus infinity to the z-score
  • One-Tailed--from the z-score to positive infinity
  • Two-Tailed--scores more extreme (i.e., further from the middle) than the z-score
  • Middle--scores less extreme (i.e., closer to the middle) than the z-score
 
File:
© 1999, Duxbury Press.