Normal Distribution

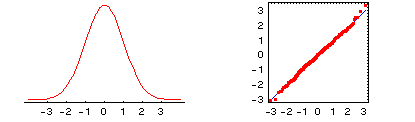
For comparison, here is the standard normal density function (on the left) and the quantile-quantile plot (on the right) for a random sample of 500 observations from that normal distribution. Note that the quantile points lie on top of or very near the line defined by the mean and the standard deviation of the sampled data values.

Chi-Square Distribution

A common deviation from normality is for data to have more observations in one "tail" of the distribution than would be expected for the normal distribution. Such distributions are referred to as skewed. One such distribution is the chi-square distribution. (The particulars of the chi-square distribution are of no concern here, but for the curious, the chi-square distribution results from squaring values from a standard normal distribution and then, possibly, adding several together.) Of importance here is that this distribution has a positive skew because of more extreme observations above the mean than below. This appears in the quantile-quantile plot with the data quantiles forming a line steeper than the blue line determined by the mean and standard deviation. At the lower end, the density of the chi-square is "squished," which appears in the quantile-quantile plot with the data quantiles forming a line fatter than the blue line. This pattern in the quantile-quantile plot is characteristic of skewed distributions, whether or not it is a chi-square distribution.

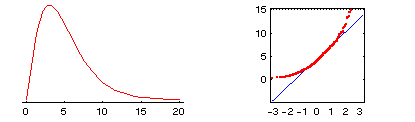
NOTE: Whenever the quantile-quantile plot shows a steeper-than-expected set of values, the mean (and other measures based on minimizing sums of squares) may be very misleading because of the greater number of extreme observations.

Uniform Distribution

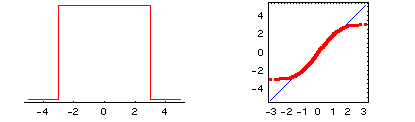
The uniform distribution has equal probability for any data value between two given end points. Its tails are obviously shorter than those for the normal distribution. This appears in the quantile-quantile plot as two flat sections for the data quantiles at either end. Such flat sections are characteristic of distributions which have fewer extreme observations than expected for the normal distribution. While they clearly are not normal distributions, they do not pose any particular statistical problems.

Cauchy Distribution

Some data distributions have the same general shape as the normal, but have thicker tails (i.e., more extreme observations) on both sides. One such distribution is the Cauchy, which results from dividing values from two standard normal distributions. The extreme tails appear as two steep sections in the data quantiles at either end of the quantile-quantile plot.

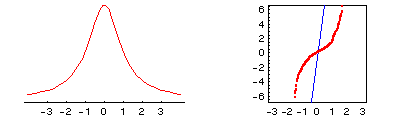
NOTE: Deviations in the quantile-quantile plot indicate that the data are seriously nonnormal in ways that can be very damaging to statistical procedures that assume normality.